-
本文的金融系统模型是Caetano M A L在2011年基于化学反应提出的一类新型模型,已被证明充分吻合实际数据.之前已有很多作者研究过此类金融系统[1-3],但本文所研究的金融系统的风险评估模型的具体动力行为还未曾被研究过.
研究系统的同步和稳定有很多方法,比如自适应控制[4]、模糊控制[5]、脉冲控制[6]、误差反馈控制[7]等等.由于脉冲控制的不连续性质可以有效节约能量,最近已有很多研究人员将其与其它同步方法结合起来研究系统同步,例如:把自适应控制和脉冲控制结合起来,称为自适应脉冲控制[8];把模糊控制与脉冲控制结合起来,称为模糊脉冲控制[9]等等.
本文先研究用脉冲控制来使系统达到同步,再研究用自适应脉冲控制的方法使得系统达到同步稳定,并给出两种方法的利弊,最后给出数值模拟验证本文同步方法的有效性.
HTML
-
通常把一个固定时刻的脉冲微分方程描述为
其中:x∈ℝn在t=τk处左连续;离散集合{τk}为脉冲时刻,并且满足0<τ1<τ2<…<τk<τk+1<…,τk→∞,k→∞时,函数f:ℝ+×ℝn→ℝn是连续的.
定义1 函数V:ℝ+×ℝn→ℝ+称为属于V0的,如果满足
(ⅰ) V在区间(τk-1,τk]×ℝn上连续,且对每一个x∈ℝn,都有极限
存在,其中k=1,2,….
(ⅱ) V关于x是局部Lipschitz连续的.
定义2 对于(t,x)∈(τk-1,τk)×ℝn,定义V∈V0上的右上Dini导数为
定义3 称函数α∈κ,如果α∈[ℝ+,ℝ+],α(0)=0且α(x)关于x严格单调递增.
引理1[10] 若满足以下3个条件:
(ⅰ) V:ℝ+×Sρ→ℝ+,ρ>0,V∈V0, D+V(t,x)≤g(t,V(t,x))且t≠τk;
(ⅱ) 存在一个ρ0>0使得x∈Sρ0,且对所有k,有x+U(k,0)∈Sρ0,并且
(ⅲ) α(‖x‖)≤V(t,x)≤β(‖x‖),其中:(t,x)∈ℝ+×ρ;α,β∈κ.
则若比较系统(4) 的平凡解有稳定性,那么其相应系统(1) 的平凡解也具有稳定性.
引理2[11] 若g(t,ω)=
$ {\dot \lambda } $ (t)ω,λ∈C1[ℝ1,ℝ1], ϕk(ω)=dkω,且对所有k有ω≥0,则系统(1) 的原点是渐近稳定的,如果满足V(0)=0,V(x)>0,x≠0,进一步,若集合除了{0}以外没有其他的不变集,且满足
则该非线性脉冲动力系统的零解x(t)≡0是渐近稳定的, Dc是该系统吸引域中的一个子集.
-
本文所讨论的金融模型是在可逆的化学反应的基础上构造出来的.最初的化学反应方程为y1+y2⇔y3+H,其中y1,y2,y3代表3种化学物质,H代表水.
基于此简单的化学反应,y3浓度的改变可以通过如下微分方程来描述
其中k1,k2分别代表正向反应和逆向反应的变化率系数.由此推出本文所用到的模型为:
其中a1,a2,a3,a4,a5,a6为常数.通过对比股票市场我们可以建立联系,例如变量y1代表Hang seng指数(HSI),y2代表Dow Jones指数,y3代表Ibovespa(Brazilian股票市场指数).这时HSI和Dow Jones指数通过项a6y1y2影响Ibovesopa指数,使得Brazilian指数以变化率a6升高,另一方面如果Dow Jones指数降低价值则会通过项a3y2降低Ibovesopa指数,而那些从Brazilian流出的投资,则分别通过项a3y3和a5y3使得HSI和Dow Jones指数增加.项a1a2y1+a1a4y2代表从HSI和Dow Jones指数流出的资产进入Brazilian股票市场.
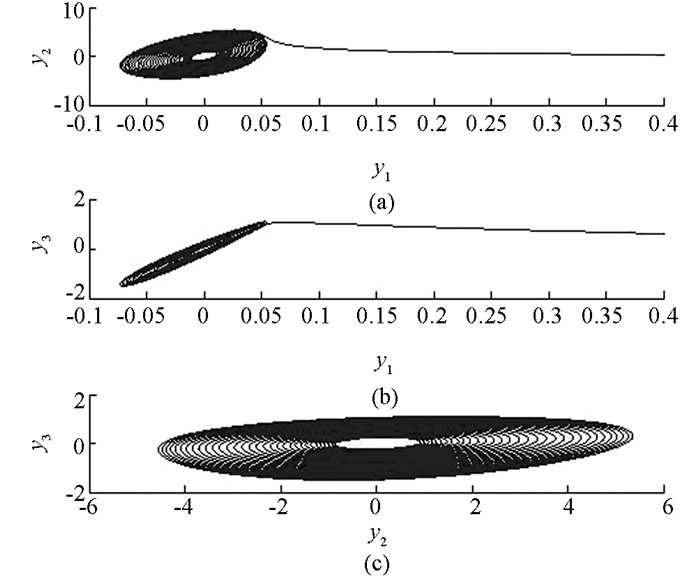
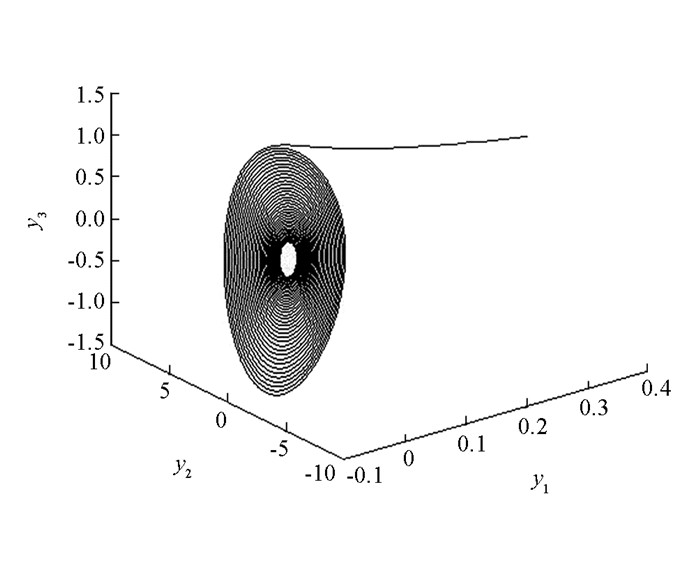
当系数a1=0.44,a2=12.31,a3=0.52,a4=0.53,a5=12.92,a6=2.34时,系统(5) 为混沌系统(图 2).从而由混沌性质可知系统(5) 的状态变量都是有界的.
-
方程(5) 为驱动系统,则其在脉冲控制下的响应系统为
其中:z∈ℝ3在t=τk处左连续且τk满足0<τ1<τ2<…<τk<τk+1<…,τk→∞,k→∞;Bk=diag(B1k,B2k,B3k)是脉冲控制常数矩阵;Bik(i=1,2,3) 是脉冲控制;e=(e1,e2,e3)T=(z1-y1,z2-y2,z3-y3)T是同步误差.
由系统(5),(6) 式可得同步误差系统:
下面找到关于脉冲控制Bik和脉冲区间(τk-1,τk)的一些充分条件使得脉冲控制响应系统(6) 和驱动系统(5) 对任意初值是全局渐近同步的.
定理1 令λ2为(I+Bk)T(I+Bk)的最大特征值,脉冲控制矩阵Bk=diag(B1k,B2k,B3k)且(I+Bk)T(I+Bk)的谱半径ρ≤1,若满足条件
则系统(6) 和系统(5) 同步.
证 令V(e)=
$ \frac{1}{2} $ eTe,当t≠τk时,因此满足引理1中的条件(ⅰ)且g(t,ω)=λ1ω.
接着再考虑当t=τk时的情况,因为I+Bk是对称的,由欧几里得范数可知ρ(I+Bk)=‖I+Bk‖,则对任意ρ0>0使得x∈Sρ0,有
则
从而满足引理1中的条件(ⅱ),且ϕk(ω)=λ2ω,显然,引理1的条件(ⅲ)也满足.因此,比较系统可写为
由引理2知,若满足对任意k且ε>1,有λ1(τk+1)+ln(ελ2)≤λ1(τk),则系统(7) 的原点是渐近稳定的,从而系统(5) 和(6) 达到同步,定理得证.
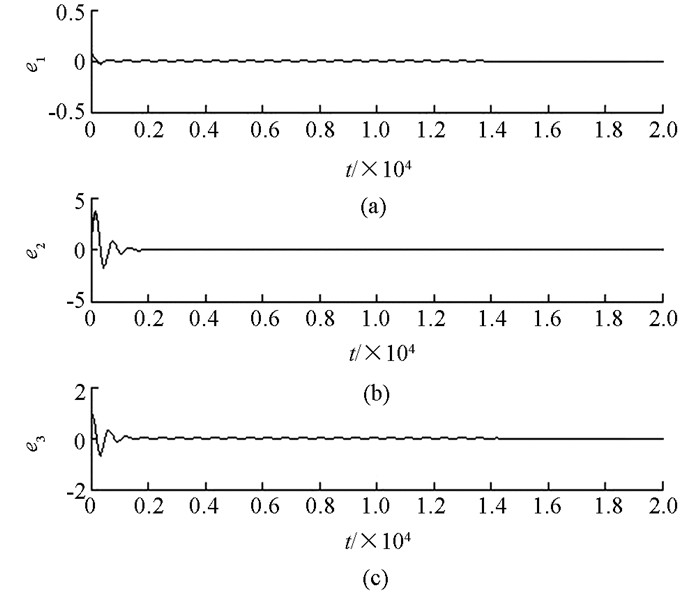
下面用数值模拟来验证脉冲控制方法的有效性.不妨设{τk}是等距的且τk+1-τk=δ>0.参数为a1=0.44,a2=12.31,a3=0.52,a4=0.53,a5=12.92,a6=2.34时,系统(5) 出现混沌状态.此时当脉冲控制矩阵Bk=diag(-0.1,-0.01,-0.18) 时,取初值y1=0.4,y2=0.3,y3=0.1,可以找到相应的ε,δ使脉冲同步误差系统(7) 的解趋于零(图 3).
-
本节将考虑通过自适应脉冲同步的方法来实现与系统(1) 的同步.
自适应脉冲控制下的响应系统为
令
其中:γi>0,i=1,2,3为任意常数;mi为自适应控制器.则误差系统为
定理2 若ρik=λmax((I+Bk)T(I+Bk))≤1,i=1,2,3,k=1,2,…,则在自适应脉冲控制器{ui;Bk;τk}下,驱动系统(5) 与响应系统(8) 为全局渐近同步的.
证 令
$ V = \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e + }}\frac{1}{2}\sum\limits_{i = 1}^3 {\frac{1}{{{\gamma _i}}}{{\left( {{m_i} + l} \right)}^2}} $ ,l为一个正常数.当t≠τk时,又l为正常数,故Q为负定矩阵,所以通过选择适当的l可以使得
$ \dot V \le-{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}} $ .当t=τk时,
定义集合K={
$ {\dot V} $ =0,t≠τk,k=1,2,…}∪{V(τk+)=V(τk),t=τk},k=1,2,…并且集合Ω={(e,m)∈ℝn×ℝn:e(t)=0,m=m0∈ℝn}为包含在K中的最大不变子集,由文献[12]推论5.1可知,系统(9) 的轨迹收敛到集合Ω,也就是说当t→∞时,e(t)→0,m→m0,故系统(5) 与系统(9) 达到同步.选取参数a1=0.44,a2=12.31,a3=0.52,a4=0.53,r1=8.92,r2=0.34,r3=0.017且脉冲控制矩阵Bk与初值都不变时,系统(9) 的解趋于零,即系统(5) 与系统(8) 达到同步(图 4).
注1 自适应脉冲控制对脉冲区间并没有特殊的要求,而对于一般的脉冲区间如何获得最大的脉冲区间则是一个很重要的研究课题.本文中一般脉冲控制的脉冲区间的极限估计是自适应脉冲方法的基础,当脉冲增益固定时,就会获得最大脉冲区间,简便的脉冲控制也能减少能量的消耗.
注2 自适应控制具有设计简便的优点,但连续控制需要更多的能量,而一般的脉冲控制却可以节省很多能量,本文新的自适应脉冲控制则结合了自适应脉冲控制和脉冲控制的优点,即设计简便且节约能量.故本文中给出的方法可以运用到很多领域,如通信安全和商业系统.
注3 在自适应脉冲控制中,脉冲控制消耗的能量少于一般的脉冲控制.尽管如此,连续的自适应控制需要持续的能量,所以自适应脉冲控制损耗的能量不一定比脉冲控制少.因此从节约能源的观点来看,如何构造更加有效的自适应脉冲控制是很有必要的,这也需要我们进一步研究.
-
首先,对一类具有风险评估的金融系统模型提出了一种脉冲同步方法,通过比较原则得到一些同步的充分条件,估计出达到脉冲同步的最大脉冲区间,并通过数值模拟来验证该方法的有效性;接着又介绍了一种自适应脉冲同步方法,给出达到同步的一些充分条件,并利用数值模拟来验证该理论结果的有效性.这些结果对于实现金融系统和股票市场的稳定同步是非常有用的.







 DownLoad:
DownLoad: