Scalarization for Approximate Proper Efficiency Solutions of Vector Optimization Problems on Real Linear Spaces

本文中，设X和Y是两个实线性空间，X^*和Y^*分别为X和Y的线性对偶空间. A⊆Y，K⊆Y是一个非平凡的凸锥.

K是点锥，如果K∩(-K)={0}. cone(A)，conv(A)和vcl(A)分别表示A的生成锥、凸包、向量闭包. cor(A)，icr(A)分别表示A的代数内部和相对代数内部. K⁺，K^s+分别表示K的正极锥和严格正极锥.其定义为：

本文将考虑如下向量优化问题：

(VOP)

其中：E⊆X且E≠∅，f：E→Y.

设ε∈K\{0}，下面给出文献[14]中引进的4种近似解的概念.

定义1^[14]  称x₀∈E为(VOP)问题的ε-有效解，若

当K是代数内部非空的，称x₀∈E为(VOP)问题的ε-弱有效解，若

定义2^[14]  称x₀∈E为(VOP)问题的ε-Hurwicz真有效解(ε-HuV)，若

称x₀∈E为(VOP)问题的ε-Benson真有效解(ε-BeV)，若

文献[14]中针对(VOP)问题研究了ε-HuV与ε-BeV之间的关系，具体结果如下.

引理1^[14]  1)若x₀是(VOP)问题的ε-HuV，则x₀是(VOP)问题的ε-BeV.

2) 假设-ε∈K.若x₀是(VOP)问题的ε-BeV且cone(f(E)-f(x₀)+K+ε)是凸集，则x₀是(VOP)问题的ε-HuV.

下面我们说明ε-HuV事实上是精确的有效解，在一定条件下，也是Benson真有效解.

引理2  1)若x₀是(VOP)问题的ε-HuV，则x₀是(VOP)问题的有效解.

2) 假设K为点凸锥，若x₀是(VOP)问题的ε-HuV，且cone(f(E)-f(x₀))和cone(f(E)-f(x₀)+K)都是闭集，则x₀为(VOP)问题的Benson真有效解.

证  1)因为x₀是(VOP)问题的ε-HuV，故

从而有

因此

所以，x₀是(VOP)问题的有效解.

2) 因为x₀是(VOP)问题的ε-HuV，故由(1)式可得

又cone(f(E)-f(x₀))是闭集.从而有

另一方面，K是点凸锥，所以有

又由cone(f(E)-f(x₀)+K)为闭集，从而有

故x₀为(VOP)问题的Benson真有效解.

注1  1)若x₀∈E满足(1)式，但K不为点锥，则x₀不一定为(VOP)问题的Benson真有效解(见例1)；若x₀∈E满足(1)式，但cone(f(E)-f(x₀))或cone(f(E)-f(x₀)+K)不是闭集，则x₀不一定为(VOP)问题的Benson真有效解(见例2).

2) 当K为点锥时，引理1 2)中的假设-ε∈K和ε∈K意味着ε=0，但文献[14]中要求ε∈K\{0}，这表明当K为点锥时，条件-ε∈K是不合理的.由此可知，在点凸锥这个条件下，要由ε-BeV得到ε-HuV，必须要求ε=0，即要由近似解得精确解，必须要有ε=0这个条件.

例1  设E⊆ $ {{\mathbb{R}}^{2}}$，f：E→ $ {{\mathbb{R}}^{2}}$，E={(x₁，x₂)^T∈ $ {{\mathbb{R}}^{2}}$|x₂=x₁，x₁≥0}，f(x)=x，K={(x₁，x₂)^T∈ $ {{\mathbb{R}}^{2}}$|x₂≥0}，x₀=(0，0)^T∈E.可得到

但

所以，x₀不是(VOP)问题的Benson真有效解.

例2  设E⊆ $ {{\mathbb{R}}^{2}}$，f：E→ $ {{\mathbb{R}}^{2}}$，E={(x₁，x₂)^T∈ $ {{\mathbb{R}}^{2}}$|x₁≥0，x₂≥0}，f(x)=x，K={(x₁，x₂)^T∈ $ {{\mathbb{R}}^{2}}$|x₂≥-x₁(x₁≤0)，x₂＞-x₁(x₁＞0)}，x₀=(0，0)^T∈E.我们可得到

但

所以，x₀不是(VOP)问题的Benson真有效解.

本节在文献[15]的基础上给出了实线性空间中一种新的近似真有效解，并在引理3的基础上给出了其对应的线性标量化.

设非空集合C⊆Y，若对任意的α≥1，有αC⊆C，则称集合C是co-radiant集.令C(ε)=εC，∀ε＞0. C(0)= $ \mathop {\rm{U}}\limits_{\mathit{\varepsilon }{\rm{ > 0}}} $C(ε)^[2].

关于非空集合Q⊆Y的支撑函数σ_Q：Y^*→ $ \mathbb{R}$∪{+∞}为σ_Q(y^*)= $ \underset{\mathit{y}\in \mathit{Q}}{\mathop{\rm{sup}}}\, ${y^*(y)}，∀y^*∈Y^*.

定义3^[11]  设E⊆X，f：E→Y，若cone(f(E)+K)为凸集，则称f(E)是在E上关于K的广义次类凸函数.

定义4^[15]  称x₀∈E是(VOP)问题关于C的ε有效解，若

称x₀∈E是(VOP)问题关于C的ε弱有效解，若

定义5^[15]  设ε≥0.称x₀∈E是(VOP)问题关于C的ε真有效解，若

引理3^[14]  设M，K是Y上的两个非平凡的向量闭凸锥，M，K均相对代数内部非空，K⁺代数内部非空.若M∩K={0}，则存在函数l∈Y^*使得

进一步有

定义6  称x₀∈E是(VOP)问题关于C的ε-Hurwicz真有效解(ε-HuV)，若

称x₀∈E是(VOP)问题关于C的ε-Benson真有效解(ε-BeV)，若

注2  1)定义6中的关于C的ε-Hurwicz真有效解是在定义2的基础上得到的.与引理1的结果1)类似可得到：若x₀是(VOP)问题关于C的ε-HuV，则有

从而

所以x₀是(VOP)问题的有效解.

2) 若x₀是(VOP)问题关于C的ε-BeV，则x₀不一定是(VOP)问题关于C的ε有效解，见例3.

在引理1的基础上我们可得到如下结果.

定理1  1)若x₀是(VOP)问题关于C的ε-HuV，则x₀是(VOP)问题关于C的ε-BeV.

2) 假设0∈C，若x₀是(VOP)问题关于C的ε-BeV且cone(f(E)-f(x₀)+C(ε))为凸集，则x₀是(VOP)问题关于C的ε-HuV.

注3  1)定理1 1)的逆命题不一定成立，见例3.

2) 若x₀是(VOP)问题关于C的ε-BeV，则由假设0∈C，我们可得x₀是(VOP)问题的有效解.这是因为，若x₀是(VOP)问题关于C的ε-BeV，则有

又0∈C，所以有

故x₀是(VOP)问题的有效解.特别地，以K+ε来代替C(ε)，则有0∈C(ε)=K+ε，-ε∈K.当K为点凸锥时，有ε=0，这时，近似解之间的关系就转化为精确解之间的关系了.

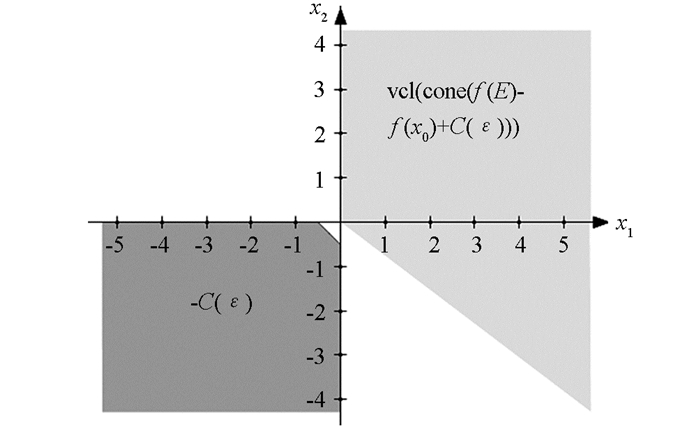
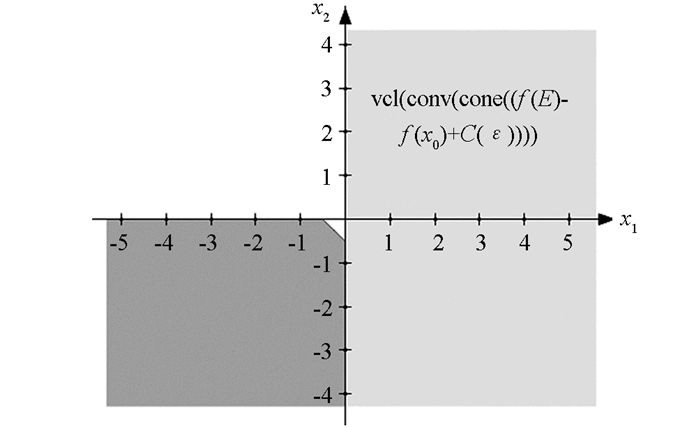
例3  设E⊆ $ {{\mathbb{R}}^{2}}$，f：E→ $ {{\mathbb{R}}^{2}}$，E={(x₁，x₂)^T|x₁=0，x₂≥0}，f(x)=x，C={(x₁，x₂)^T|x₁≥0，x₂≥0，x₁+x₂≥1}，取ε= $ \frac{1}{4}$，x₀= (0，$ \frac{1}{4}$)，则我们可以得到：x₀是(VOP)问题关于C的ε-BeV，但不是(VOP)问题关于C的ε-HuV(如图 1，2所示).

下面利用引理3建立(VOP)问题关于C的ε-BeV的线性标量化.

令

定理2  设ε≥0，x₀∈E，C是代数内部非空的凸集，f(E)-f(x₀)是在E上关于C(ε)的广义次类凸函数.若x₀是(VOP)问题关于C的ε-BeV，则x₀为标量化问题$ \underset{\mathit{x}\in \mathit{E}}{\mathop{\rm{min}}}\, $φ(f(x))的-εσ_-C(φ)最优解.

证  由x₀是(VOP)问题关于C的ε-BeV，有

所以

又由假设：f(E)-f(x₀)是在E上关于C(ε)的广义次类凸函数，得到vcl(cone((f(E)-f(x₀))+C(ε)))为凸集.所以，由引理3，存在φ∈D^s+使得

因此，有

故

所以，x₀为标量化问题$ \underset{\mathit{x}\in \mathit{E}}{\mathop{\rm{min}}}\, $φ(f(x))的-εσ_-C(φ)最优解.

注4  若0∈C且C(0)=D，则当ε=0时，定理2可以退化到文献[16]中定理4.2的结果.

定理3  设ε≥0，x₀∈E.若存在φ∈D^s+使得

则x₀是(VOP)问题关于C的ε-BeV.

证  假设x₀不是(VOP)问题关于C的ε-BeV，则存在y≠0使得

因为φ∈D^s+，故φ(y)＜0.又因

从而存在y′∈Y和序列λ_n→0⁺，使得

这表明，存在序列{α_n}⊆[0，+∞)，{x_n}⊆E和{d_n}⊆C，使得

另一方面

所以

即

当λ_n→0⁺时，有φ(y)≥0，这与前述φ(y)＜0矛盾.所以x₀是(VOP)问题关于C的ε-BeV.

注5  若0∈C且C(0)=D，则当ε=0时，定理3的结果可退化为x₀是(VOP)问题的Benson真有效解.