The Finite Element Operator Splitting Method for the Incompressible Navier-Stokes Equations

考虑下面的Navier-Stokes方程：

其中：Ω是在$ \mathbb{R}^2$上具有利普希茨连续边界的有界区域，u(x，t)∈$ \mathbb{R}$^d表示速度矢量，p(x，t)∈$ \mathbb{R}$是压力，f(x，t)是流体驱动的体积力，ν＞0为流体粘性系数， u₀是使得∇·u=0的初始速度，并且${\mathit{\boldsymbol{u}}_t} = \frac{{\partial u}}{{\partial t}} $.

对于上面给出的Navier-Stokes方程，我们引入下面的希尔伯特空间：

其中：(·，·)表示空间L²(Ω)²或L²(Ω)的标准内积，(∇u，∇u)和‖∇u‖₀为空间V的一般标量和范数.在这篇文章中，我们用字母C表示一个与时间步长和网格参数无关的正数.

设u和p满足下面的条件：

(R1) u∈C⁰(0，T；H)∩L^∞(0，T；H²(Ω))，∇p∈L^∞(0，T；L²(Ω)).

(R2a) u_t∈L²(0，T；L²(Ω)).

(R2b) u_t∈L²(0，T；H₀¹(Ω)).

(R3) ∫₀^T t‖u_tt(t)‖_-1²dt≤C.

(R4) ∫0T‖utt(t)‖V′2dt≤C.

定义三线性项c(·，·，·)为c(u，v，w)=((u·∇)v，w)，∀u∈H¹(Ω)，v∈H¹(Ω)，w∈H₀¹(Ω)，它有如下的性质：

并且定义：

步骤一  寻找解${\mathit{\boldsymbol{u}}^{n + \frac{1}{2}}} $使得

步骤二  根据(5)式解得的${\mathit{\boldsymbol{u}}^{n + \frac{1}{2}}} $求解uⁿ⁺¹和pⁿ⁺¹使得

其中δt是时间步长，满足0＜δt＜1，t_n=nδt，n=0，1，…，N-1，和$ N = \left[ {\frac{T}{{\delta t}}} \right]$.

对于方程(5)-(9)的有限元离散，我们假设T^μ={K}(μ=h)是准均匀的三角形网格剖分并且网格尺寸0＜μ＜1.定义数值格式中出现的亚格子模型为：

其中α＞0是稳定化参数，根据算子Π_h的定义，下列关系式成立：

我们定义R₀={v∈L²(Ω)：v|_K∈P₀，∀K∈T^μ(Ω)}，L_μ=R₀^2×2，L=L²(Ω)^2×2，其中P₀是常量元素K的空间，那么标准的L²-正交投影Π_μ：L→L_μ有如下性质：

下面给出亚格子稳定化的有限元算子分裂算法：

步骤一  对于给定的u_hⁿ∈V_h使得对于所有的v_hⁿ∈V_h，有

步骤二  寻找解u_hⁿ⁺¹∈V_h和p_hⁿ⁺¹∈Q_h使得对于所有的(v_h，q_h)∈V_h×Q_h有

上述提到的方法中，步骤二可以看作是一般的Stokes问题.其中有限元空间V_h⊂H₀¹(Ω)，Q_h⊂L₀²(Ω)且V_h和Q_h要求满足下面的条件：

(H1) 存在与h无关的β＞0，使得对于所有的h＞0有：

其中B_h：V_h→Q_h^′和B_h^t：Q_h→V_h^′定义如下：

(H2) 存在与h无关的γ＞0，使得对于所有的v∈H^r(Ω)和q∈H^s(Ω)以及任意的h＞0有：

(H3) 存在与δt和h无关的C＞0，使得：

定义速度误差函数为：

定理1^[4]  假设(R1)，(R2b)，(R3)和(R4)成立，那么对$ N = 0, \cdots , \left[ {\frac{T}{{\delta t}}} \right] - 1$，和足够小的δt，有下面的估计：

设有限元解$ ({\mathit{\boldsymbol{u}}_h}^{n + \frac{1}{2}}, \mathit{\boldsymbol{u}}_h^{n + 1}, \mathit{\boldsymbol{p}}_h^{n + 1})$是半离散分步解$ ({\mathit{\boldsymbol{u}}^{n + \frac{1}{2}}}, {\mathit{\boldsymbol{u}}^{n + 1}}, {\mathit{\boldsymbol{p}}^{n + 1}})$的逼近解，我们定义如下误差：

引入与有限元空间有关的误差函数：

引理1^[4]  设V_h和Q_h满足inf-sup条件(H1)，则对于u∈V满足：

定理2  设(R1)，(R2b)，(R3)，(H1)和(H3)成立，那么对于$ N = 0, \cdots , \left[ {\frac{T}{{\delta t}}} \right] - 1$和足够小的δt和h，满足：

证  让(5)式和(14)式与v_h做内积，且让两式相减得：∀(v_h，q_h)∈V_h×Q_h，

对于任意给定的(v_h，w_h，q_h)∈V_h×ker(B_h)×Q_h，由(15)式可得：

下面对(22)式右端各项估计：

因为∇·uⁿ⁺¹=0且w_h∈ker(B_h).

对于三线性项有：

在(25)式中右端第一项为0，对其余各项估计：

由定理1可知，$ {\left\| {{\mathit{\boldsymbol{e}}_c}^{n + \frac{1}{2}}} \right\|_1} \le C\delta {t^{\frac{1}{2}}}$，且由(R1)可得：

同理，可得：

将(23)，(24)，(26)，(27)，(28)式代入(22)式，并且两边同时取下确界可得：

然后将(29)式两端从0加到N-1，当时间足够小时，得：

对于足够小的δt和h，由离散的Gronwall引理，(H3)和三角不等式得证定理2成立.

结合定理1和定理2，我们可估计

推论  设(R1)，(R2b)，(R3)，(H1)，(H2)和(H3)成立，设对于所有的$n = 0, \cdots , \left[ {\frac{T}{{\delta t}}} \right] - 1 $，uⁿ⁺¹，$ {\mathit{\boldsymbol{u}}^{n + \frac{1}{2}}}$∈H^k(Ω)和pⁿ⁺¹∈H^k-1(Ω)且一致有界，那么对于$n = 0, \cdots , \left[ {\frac{T}{{\delta t}}} \right] - 1 $，以及足够小的δt＞0和h，有如下估计：

利用FreeFem++软件^[11]进行一些实验验证理论预测的正确性.

选择Navier-Stokes方程的精确解为：

其中解的区域Ω=[0, 1]×[0, 1]⊂$ \mathbb{R}$²，在这个问题中P₁^b-P₁元用于空间离散，并且取ν=1.0×10^-7，T=0.1，α=0.1 h. 表 1给出了数值结果.从表 1可知：我们的方法对空间和时间离散是一阶收敛的，同时数值结果也表明我们的理论预测是正确的.为了对比我们现在的方法和标准的有限元方法，当网格尺寸$ h = \frac{1}{{128}}$，时间步长$\mathit{\Delta }t = \frac{1}{{800}} $时，我们分别计算ν=1，0.1，0.01，0.001时方程的解.从表 2可以看出我们的有限元算子分裂算法得到的误差估计更小.

考虑一个定义在Ω=[0，2.2]×[0，0.41]上的圆柱绕流问题，其中圆心为(x，y)=(0.2，0.2)，半径为0.05，取入流速度为

并且在其他边界上满足无滑边界条件.

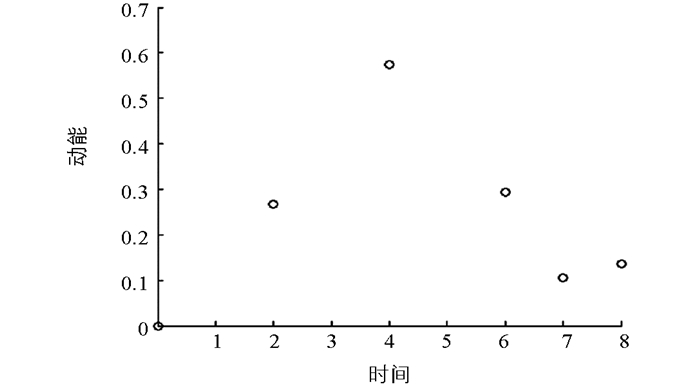
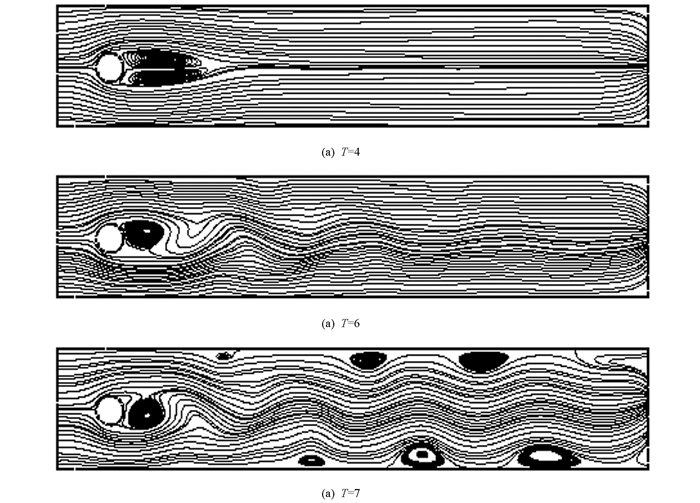
在这个问题中，Hood-Taylor元用于空间离散，粘性系数ν=0.001，网格大小为$ h = \frac{1}{{32}}$，稳定化参数α=0.1h²，时间步长Δt=0.001，分别取得最后时刻T=4，6，7. 图 1给出了区域Ω的网格剖分，图 2描述了算法关于动能和时间T的关系，图 3对比了不同时刻的流线图.

本文主要结合亚格子稳定模型和有限元算子分裂算法，理论上给出了全离散速度的误差估计，并用数值实验验证了理论的正确性和方法的有效性.对比标准的有限元方法，我们的方法得到的误差估计更小.