-
开放科学(资源服务)标识码(OSID):

-
近几十年来,由于化石燃料的过度消耗,人类面临着全球变暖和能源危机的问题,这些问题对全球经济政策、气候状况以及能源安全都产生了巨大影响。然而随着工业化和城市化的加速发展,能源需求持续增长。传统的化石燃料发电方式不仅昂贵,而且对环境造成了严重的污染和破坏,加剧了全球变暖的问题,导致气候变化引发的自然灾害频频发生[1]。为了应对这一挑战,全球各地开始寻求清洁、可持续的替代能源,其中包括太阳能、风能、生物质能、水力能以及地热能等。在这些替代能源中,太阳能光伏发电被认为是最具前景和可行的选择之一[2],并且对我国2030年前实现“碳达峰”,2060年前实现“碳中和”的目标具有重大意义[3]。太阳能光伏发电具有诸多优势,例如可再生性和环保性。然而光伏发电的一个关键挑战在于其发电量受到天气等多种因素的影响,这使得光伏发电量难以准确预测。同时传统光伏发电预测很少考虑多站点之间的关联性,为了更好地规划能源供应、电网管理和降低能源成本,对光伏集群发电预测的研究和应用具有重要的现实意义。
光伏发电预测方法主要有统计方法和机器学习方法。其中统计方法包括自回归移动平均模型(Auto Regressive and Moving Average,ARMA)、自回归积分移动平均模型(Auto Regressive Integrated Moving Average,ARIMA)和多元线性回归(Multiple Linear Regression,MLR)。ARMA模型在时间序列分析领域应用广泛,常用于处理平稳序列,进行短期负荷预测[4-5],但针对非线性数据等复杂情况时很难取得较好效果。MLR模型能够有效地应对非线性数据,并能通过多因素考虑来进行预测[6],但是存在过拟合风险并且不能捕捉时序数据的时间特征。而机器学习方法能够更好地处理复杂的非线性关系以及大量数据,能够更好地适应不同的环境变化和数据特征,具有更强的泛化能力和灵活性。通过机器学习方法进行光伏发电预测的准确率也高于利用统计方法所得的准确率[7]。常用的机器学习方法包括深度神经网络(Deep Neural Network,DNN)、支持向量机(Support Vector Machine,SVM)、随机森林(Random Forest,RF)[8]等。在文献[9-10]中,分别使用了支持向量回归模型(Support Vector Regression,SVR)与RF模型、LSTM模型与RF模型来完成光伏发电预测,说明了机器学习模型在此方面能够有效提高预测的准确率。但单一的机器学习模型存在过拟合问题,对数据分布也比较敏感,并且存在较多不确定性,导致不能在较多数据集情况中表现良好,达不到较好的综合性能。集成模型能够降低过拟合的风险,对数据分布也不敏感,具有较强的抗噪能力,以此来获得更好的性能。
因此,本文提出集成LSTM、CNN、TCN和XGBOOST单一模型的集成模型,集成模型可以聚合不同单一模型的各自特点,并结合互信息(Mutual Information,MI)集群网络结构,实现更精准的光伏集群发电预测。所提出的方法利用国家可再生能源实验室(National Renewable Energy Laboratory,NREL)的光伏发电数据集[11]作为模型输入,利用历史数据计算站点之间的互信息,形成互信息集群网络结构,再构建具有不同特点的4个经典机器学习模型,使用自适应加权策略来对单一模型进行集成,从而实现更加精准的预测以及获得更强的泛化能力。
HTML
-
在统计方法方面,Chen等[4]利用ARMA模型来预测平稳的残差序列,以提高预测精度。Colak等[12]使用ARMA模型和ARIMA模型进行多周期预测,对2个模型结果进行比较,作为确定多周期预测中最佳统计模型的结果。然而传统的统计方法对于具有复杂非线性结构的光伏发电数据不适用,于是Chen等[13]将ARIMA模型和LSTM模型进行结合,实现线性和非线性预测,可以更全面地从历史数据中提取模式,有效地减少了预测误差。
在机器学习方法方面,VanDeventer等[14]提出了一种基于遗传算法的支持向量机(GASVM)模型,用于住宅规模光伏系统的短期功率预测,先利用SVM模型对历史数据进行分类,再利用遗传算法进行优化。Pan等[15]提出了一种改进的蚁群优化(Ant Colony Optimization,ACO)算法,使用ACO算法的全局优化函数来优化SVM模型的参数,完成光伏发电预测。但SVM模型处理大规模数据集和高维特征空间的能力较弱,并且对核函数参数或惩罚参数的选择十分敏感,需要较大计算量才能确定对应参数。RF模型在文献[16]中被用来提高光伏发电预测的稳健性,研究者运用了该算法来降低特征空间的维度,并通过对多个决策树的集成来提高预测的准确性,在缺乏数据的情况下也能取得良好的效果。Abuella等[9]和Roy等[10]采用RF模型进行预测,其预测输出是单个树的预测平均值,因此提供了具有较小误差的预测结果。Izzatillaev等[17]使用人工神经网络模型(Artificial Neural Network,ANN)进行预测,并得到了更高的精度。但上述机器学习方法不能有效地探索和捕捉与预测目标密切相关的各种特征之间的深层潜在关联。
深度学习技术通过扩展神经网络的深度,能够更有效地挖掘复杂数据中的非线性结构,并从中学习到更具性能的特征表示。Kong等[18]使用递归神经网络模型(Recurrent Neural Network,RNN)来减轻负荷预测的不确定性。但由于梯度消失或爆炸问题,RNN模型难以维持中长期依赖性。针对此问题,LSTM模型通过引入门控机制来解决,利用存储单元来保持时间相关性,其能够有效地捕捉长期依赖关系,并且对序列数据的建模能力更加强大。在文献[10, 13, 19-22]中都使用了LSTM模型。此外,Deng等[23]提出了一种具有时间认知的多尺度卷积神经网络模型(Multi-Scale Convolutional Neural Network with Time-Cognition,TCMS-CNN),该模型基于多尺度卷积的深度卷积神经网络模型(Multi-Scale Convolutional Neural Network,MS-CNN)提取不同层次的特征,并将其融合到网络中。同时还设计了一种创新的时间编码策略,有效地增强了序列模型的时间认知能力[24]。
然而,单一机器学习模型泛化能力有限,不能很好地捕捉复杂的非线性关系,缺乏足够的灵活性。针对此问题,利用集成学习的方法,能够有效实现更加稳健、精准的预测。在电力方面,Wang等[25]使用了集成学习方法来提高用电量预测的精准度。集成学习方法能够增强模型的泛化能力,面对复杂的非线性关系数据也能较好地捕捉其中的特征,面对噪声和异常值也有较强的容忍性、良好的稳健性和更高的预测精度。同时,传统的电力预测模型一般仅考虑单个站点的相关影响因素,例如发电量、天气及地理位置等,并未考虑多个发电站之间的相关性。多站点间发电量的相关性揭示了不同发电站之间发电量变化的相互影响和依赖关系,这种相关性不仅可以用于预测特定站点的发电量,还可以优化发电站的运营策略,降低风险,为新能源发电系统的规划和建设提供参考依据,对提高发电系统的效率和可靠性具有重要意义。
-
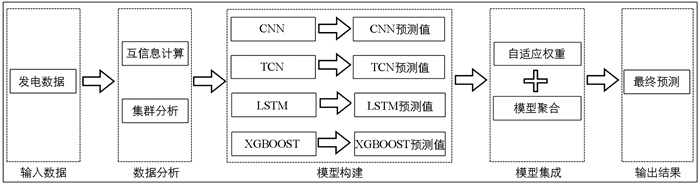
图 1对本文集成模型总体结构进行了说明。该模型将发电量数据作为输入,首先分析发电站站点之间的网络结构,利用历史发电量来计算发电站之间的互信息,衡量站点之间的相关性,借此构成具有不同集群的网络结构,然后再构建具有不同特征的4个单一深度学习模型进行预测,根据预测结果完成权重自适应计算并实现模型集成,最后输出最终预测结果。接下来将先对真实数据集进行分析,再介绍4种单一模型以及集成模型。
-
数据来源于美国国家可再生能源实验室网站(www.nrel.gov)所提供的光伏发电量数据,选取美国东部阿拉巴马州137个站点在2006年的光伏发电量作为实验数据。
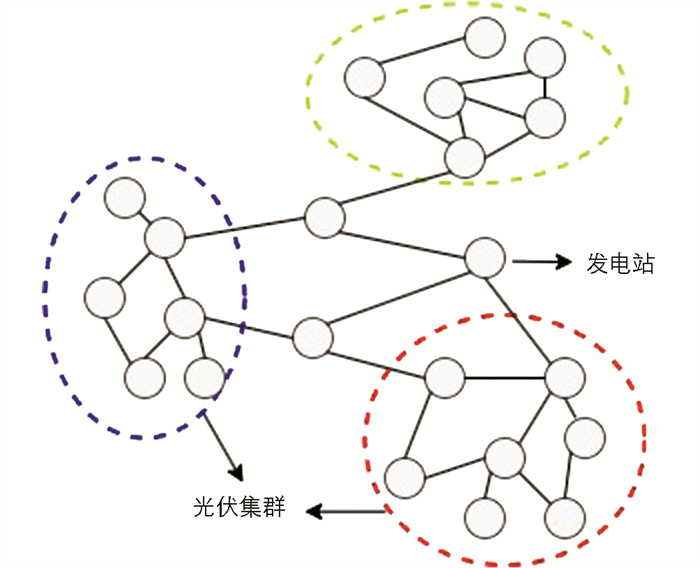
传统发电预测一般考虑单个发电站的相关影响因素,未考虑多个发电站之间的相关性。因此,本文利用互信息构建网络结构。所有发电站之间的互信息网络结构如图 2所示,节点代表发电站,利用历史发电量数据计算互信息来衡量发电站之间的相关性并作为边的权重。互信息的计算公式为:
式中:X和Y为2个离散的随机变量;P(x,y)为X和Y的联合概率分布;P(x)和P(y)分别为对应的边缘概率分布。
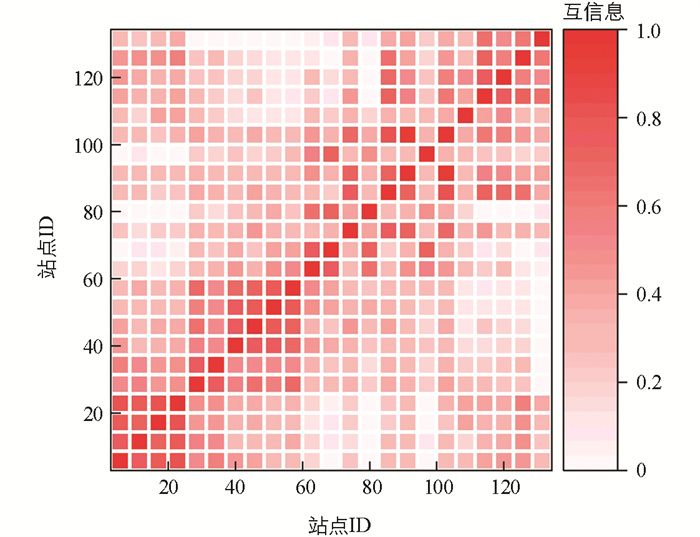
得到所有发电站之间的互信息网络结构后,通过分析对应互信息热力图(图 3),能够根据互信息将发电站分为多个集群(如图 2中虚线圈代表一个集群),并从中选取站点,利用与其相关性较高的站点发电量作为特征来进行集群发电预测。
-
CNN已经在诸如图像和视频识别、图像分类、图像处理、医学图像分析和自然语言处理等领域取得了巨大成功。除了这些领域之外,CNN在基于时间序列数据领域也日益受到青睐,这主要归因于它具备处理多通道输入数据的能力[26]。其中输入数据f和卷积核g的卷积运算数学表达式如下:
式中:S(i,j)为卷积运算的结果;m,n为卷积核的尺寸。通过卷积操作能够实现对输入数据的特征提取,从而在时间序列分析、行为识别、交通流量预测等任务中展现出优越的性能。
-
XGBOOST[27-28]是一种迭代训练多个决策树的梯度提升树算法。在每一轮迭代中XGBOOST训练一棵新的决策树,该决策树校正前一棵树的残差,然后将它们的输出进行聚合以进行预测。模型的最终输出是多个决策树输出的累积和,每个决策树的贡献由学习率控制。这种策略使其能够通过集成多个决策树来提高预测性能,并且具有较高的泛化能力。对于第i个样本的预测值,它可以表示为所有树的输出累积:
式中:K为树的数量;fk(xi)为样本xi的第k棵树的输出。在训练模型方面,定义了损失函数和正则化项,旨在使得损失函数最小化,以下是目标函数表达式:
式中:l为损失函数,计算预测值和真实值之间的误差;Ω(fk)为正则化项,控制每棵树的复杂度。
-
作为RNN的一种变体,LSTM于1997年被提出[29]。LSTM的结构包括1个输入门、1个遗忘门和1个输出门,通过控制这3个门的开闭程度,LSTM能够学习需要存储、丢弃和读取的信息。输入门负责确定新信息的重要性,遗忘门决定旧信息的保留程度,而输出门则控制当前单元状态的输出。通过这种机制,LSTM能够有效地长期记忆序列中的重要信息,并同时提取短期特征,使得网络更加适应序列数据的处理需求[30]。LSTM的数学表达式如下:
其中:f(t)为遗忘门的输出;i(t)为输入门的输出;o(t)为输出门的输出;g(t)为候选记忆细胞的输出;c(t)为该时刻的细胞状态,其根据输入门的输出和遗忘门的输出,更新细胞状态,新的细胞状态由当前输入和上一时刻的细胞状态加权求和得到;σ为激活函数;w,b为相应门的权重矩阵和偏置。
-
TCN[31]是一种专为序列建模而设计的深度学习架构。不同于传统的RNN,TCN采用CNN来捕捉序列中的长期依赖关系。每层卷积层包含激活函数以及残差连接,以下是其运算表达式:
式中:Xt=(x1,x2,…,xT)为输入序列;Yi=(y1,y2,…,yT)为输出序列;H(Xt)为卷积层输出。TCN中使用的残差连接机制有助于缓解梯度消失和爆炸问题,提高了模型的稳定性和收敛速度。
-
自适应聚合集成学习[31]通过自适应地调整每个基础模型的权重,可以有效地提高模型的泛化能力和灵活性,并能够很好地平衡各个模型的性能,在降低过拟合风险的同时也能提升预测效果。自适应聚合权重的计算表达式为:
其中:Ert(h)为第n次迭代时第t个基本模型的单独损失;Alt(n)为到第n次训练迭代时第t个基本模型的累积损失;εt(n)为第t个基本模型的集成权重;
$\delta=\sqrt{1 / \ln T}$ 为在训练过程中控制集合的聚合权重的平衡因子;T为最大训练迭代次数。
2.1. 数据分析
2.2. 卷积神经网络(CNN)
2.3. 极端梯度提升(XGBOOST)
2.4. 长短期记忆网络(LSTM)
2.5. 时序卷积网络(TCN)
2.6. 集成模型
-
根据发电站互信息集群网络结构,从4个集群中选取4个发电站进行光伏集群发电预测,将与被选择站点相关性高的站点发电数据作为其特征来完成预测。首先对数据集进行归一化处理,再利用滑动窗口方法将数据集构造成相应的训练数据和对应标签,最后将数据集按照8∶1∶1的比例划分成训练集、验证集和测试集。
-
选择CNN、TCN、LSTM和XGBOOST模型来进行集成学习,所有模型参数如表 1所示。
-
为了评估所提出的集成方法,设计了以下2组实验:
1) 单一模型与集成模型的比较。
2) 预测模型的超参数分析。
-
实验利用均方误差(Mean Square Error,MSE)和平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)评估模型的预测能力,这些评价指标被广泛应用于时间序列预测方面,都具有较为直观的解释性,以下是其计算公式:
其中:n为样本总数;yi为第i个真实值;
$\hat{y}_i$ 为第i个预测值。EMSE和EMAPE的值越小,说明预测值与真实值越接近,对应模型预测精度越高。 -
在此实验环节,将单一模型即CNN、XGBOOST、LSTM和TCN与集成模型的预测能力进行对比,实验结果如表 2和表 3所示。其中表 2是基于评价指标EMSE得到的,表 3是基于评价指标EMAPE得到的。根据实验结果,本文还通过Wilcoxon符号秩检验和Friedman检验进行了统计分析[32-33],以下是分析结果:
1) 集成模型针对2个指标都表现出较好的预测结果,在4个站点的单步预测指标都优于其余4个单一模型的指标。
2) 集成模型在4个站点的预测中,指标EMSE始终低于10.00,最低可至0.000 2,指标EMAPE始终低于112.06,最低可至0.19。
集成模型在预测精度上相较单一模型有明显提升,针对不同光伏发电站的发电量预测也有较强的泛化能力。
-
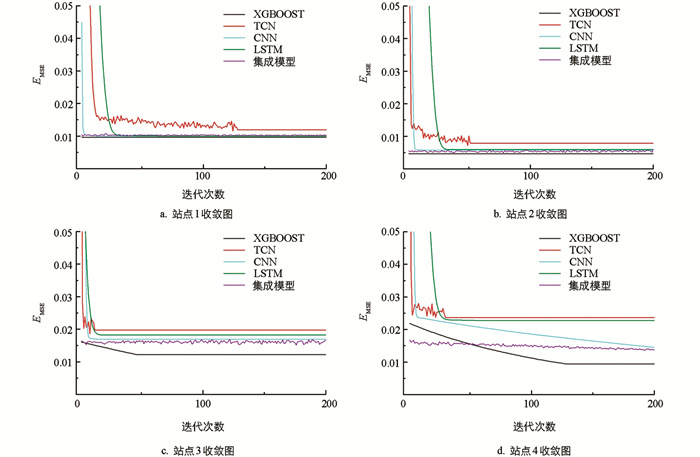
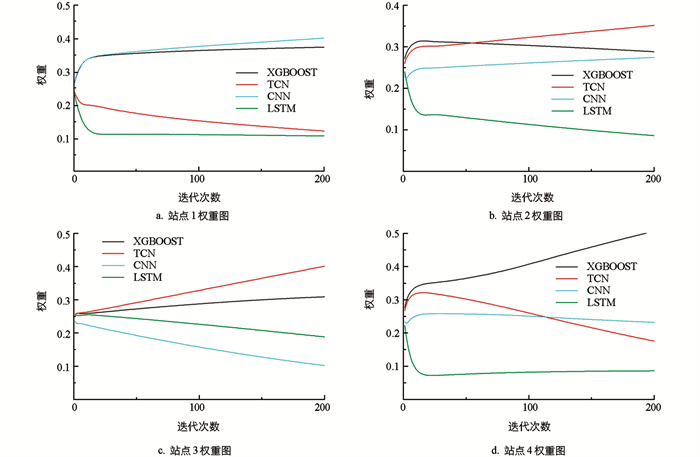
本实验环节对集成模型的集成过程和性能进行了可视化,图 4和图 5分别是集成模型对4个站点发电量预测的收敛曲线图和权重图,根据以下可视化信息,可以得出以下结论:
1) 所有模型在不同站点的数据下均能够随着训练次数的增加逐渐收敛,并得到最优预测结果,但单一模型不能在所有情况下都具有较好的预测结果。
2) 集成模型能够根据误差自适应调整权重,在4个发电站的发电量预测中获得良好的预测结果。
3) 集成模型相较单一模型,通过自适应权重计算,不仅在多种情况下能够拥有较好的性能,并且具备良好的灵活性。
3.1. 数据集处理
3.2. 模型参数
3.3. 实验设置
3.3.1. 实验设计
3.3.2. 评价指标
3.4. 单一模型与集成模型的比较
3.5. 集成模型分析
-
本文提出了一种基于混合深度学习的光伏集群发电预测模型。该模型首先根据历史数据构建互信息集群网络结构,基于此对经典单一深度学习模型CNN、TCN、LSTM和XGBOOST进行构建并完成初步预测。然后再根据其预测结果实现自适应权重计算,完成集成学习得到最终预测结果。集成模型相较单一模型拥有良好的灵活性和泛化能力。通过实验证明,该集成模型在不同光伏发电站的发电量预测中,其预测精度较单一模型都有显著提升。本文主要集中在利用多个发电站的发电量数据进行预测,并没有考虑气象等因素对发电量的影响。在之后的研究中,将考虑地理位置或气象等因素对发电量的影响,以提高模型在各种复杂环境条件下的准确性和灵活性,为实际应用提供更可靠的预测结果。






 DownLoad:
DownLoad: