On Solution of Cooperative Game Based on Symmetric Alternating Direction Method with Positive Indefinite Proximal Regularization

合作对策(N，v)的核心是非劣的分配的集合.对于分配x =(x₁，x₂，x₃…x_n)∈$ \mathbb{R}$ⁿ，称集合

为合作对策(N，v)的核心.其中v(S)表示联盟S中各局中人通过合作所得的最大利益，x(S)是分配给联盟S的值.由(3)式易知，核心C(v)是$ \mathbb{R}$ⁿ中的有界闭凸集.

核心具有帕累托最优性、稳定性、匿名性、超可加性等好的性质.所以核心中的分配不仅满足个体理性和集体理性，而且满足联盟理性，即任何联盟离开核心所得收益都不超过在核心中的分配.因此在核心中的每个局中人都会努力保护核心成立，但是核心作为合作对策的解并不总是存在的，即使存在也不能保证唯一性，所以如何取得属于核心中的合作对策的解是一个值得研究的课题.

Nguyen提出了最公平核心的概念：假设合作对策(N，v)具有非空核心，则最公平核心是如下优化问题的解：

其中：ψ =(ψ₁，ψ₂…ψ_n)^T，ψ_i(i=1，2，…n)是局中人i的Shapley值

(4) 式中|S|是联盟S中局中人的个数，最公平核心属于核心且与Shapley值有着最近的欧氏距离，即最公平核心是欧氏范数下ψ在C(v)上的投影：

由于C(v)非空且为有界闭凸集，所以投影P_C(v)(ψ)存在且唯一，即最公平核心是唯一的，这里也体现了最公平核心的唯一性.

文献[8]通过生成随机最小支撑树的数值实验表明随着合作对策中局中人个数的增加，问题所具有的约束条件呈指数增长，此时求解最公平核心问题的难度不亚于寻找核心.而对于这种高维问题，求解凸二次规划问题的交替方向法有着非常显著的成效，因此把求解最公平核心问题转化为凸二次规划问题，再用交替方向法进行求解是本文的想法.

考虑到联盟成立的个体合理性条件，求解合作对策的最公平核心与下列凸优化问题等价：

在文献[9]中，通过添加人工变量y ∈$ \mathbb{R}$^m，将上述凸优化问题转化为以下凸二次规划问题：

其中

易知X，Y是简单闭凸集.矩阵A ∈$ \mathbb{R}$^m×n，每行非零元素均为1，m表示n个局中人组成的联盟个数，每行1的位置由联盟中的局中人是否被选择决定，即1表示局中人在联盟中，0表示局中人不在联盟中. b =(b₁，b₂…b_m)^T∈$ \mathbb{R}$^m，对∀i∈{1，2，…m}，b_i等于矩阵A的第i行对应的联盟S_i的支付v_i.

在文献[9]中采取非精确平行分裂算法(INPSALM)^[16]求解问题(5)，算法在运算中不能充分运用已知信息，且算法无法在已知信息较少的情况下运行.为此，本文给出了一种带有正不定临界项的对称交替方向法求解凸二次规划问题(5).

首先将问题(5)转化为变分不等式的形式.

定义可微函数θ：$ \mathbb{R}$ⁿ→$ \mathbb{R}$如下

故得到(5)式的Lagrange函数为

其中λ ∈$ \mathbb{R}$^m是Lagrange乘子.寻找(6)式的鞍点ω^*=(x^*，y^*，λ^*)^T使得

将其代入(6)式得到

整理即得变分不等式结构：

其中

求得的鞍点ω^*∈Ω即是使得变分不等式(7)成立的点.

在将原约束问题转化为无约束问题时，现实中的原问题不一定都是强凸函数，同时为了加快算法的收敛速度，考虑(7)式的增广Lagrange函数

其中：λ ∈$ \mathbb{R}$^m为Lagrange乘子，β>0是罚因子，即对违反等式约束的条件作出惩罚.应用文献[15]中算法(PIDSADMM)求解变分不等式(7)，算法如下：

Step 1：给定ε>0，α∈(-1，1)，r≥β>0，选取初始点ω⁰=(x⁰，y⁰，λ⁰)∈Ω，令k=0

Step 2：对任意的ω^k=(x^k，y^k，λ^k)∈Ω，计算x^k+1∈X和${\boldsymbol{\lambda }^{k + \frac{1}{2}}} \in {\boldsymbol{\lambda }^m} $，满足

Step 3：计算y^k+1∈Y和λ^k+1∈λ^m，满足

Step 4：如果e_k=max{‖ Ax^k+1- y^k+1- b ‖_∞，‖βA (x^k+1- x^k)‖_∞}≤ε，迭代停止.

此时ω^k+1=(x^k+1，y^k+1，λ^k+1)可作为凸二次规划问题(5)的解，否则令k=k+1，转至Step2.

在这里，D₀=(τr-β) I_m，$\tau \in \left[ {\frac{{{\alpha ^2} - \alpha + 4}}{{{\alpha ^2} - 2\alpha + 5}}, 1} \right)$.其实Step3中y的表达式等价于

其中q_k=β(Ax^k+1- y^k- b)- ${\boldsymbol{\lambda }^{k + \frac{1}{2}}} $.

PIDSADMM算法收敛性已经在文献[15]中证明.容易证明由PIDSADMM算法计算出的结果即为凸二次规划模型(5)的解，且Lagrange乘子在一次迭代中更新两次，具有较好的收敛率.对于一个固定的r只需要选取适当的临界系数使得临界项在目标函数中占有较小的比重，临界项中矩阵D₀的不定性可允许算法在可行域有较大的最优步长从而加快算法的数值收敛.对于给定的初始点(y^k，λ^k)，通过上述算法产生下一个迭代点ω^k+1=(x^k+1，y^k+1，λ^k+1)，即在已知初始信息较少的情况下问题仍然可以解决，且变量在迭代过程中交替更新的方式使得信息应用更加充分.由于X，Y均为有界闭凸集合，所以以上算法是可以计算的.

本节运用PIDSADMM算法求解一对合作对策的最公平核心的示例来说明算法的可行性.与文献[16]中的算法运算的结果进行对比分析可知算法的有效性.

例1   求解下列一对合作对策的最公平核心，其特征函数v满足：

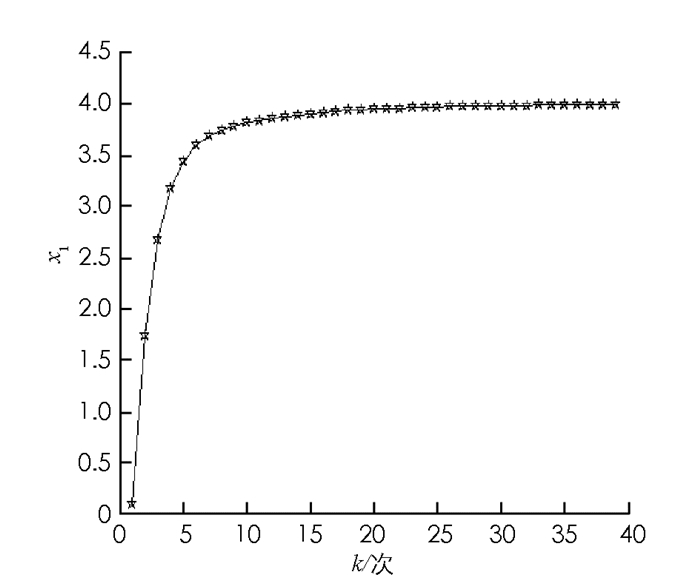
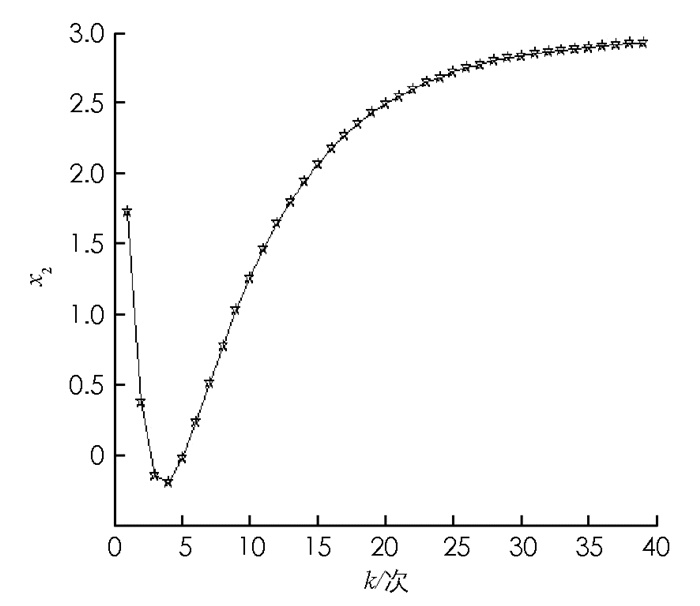
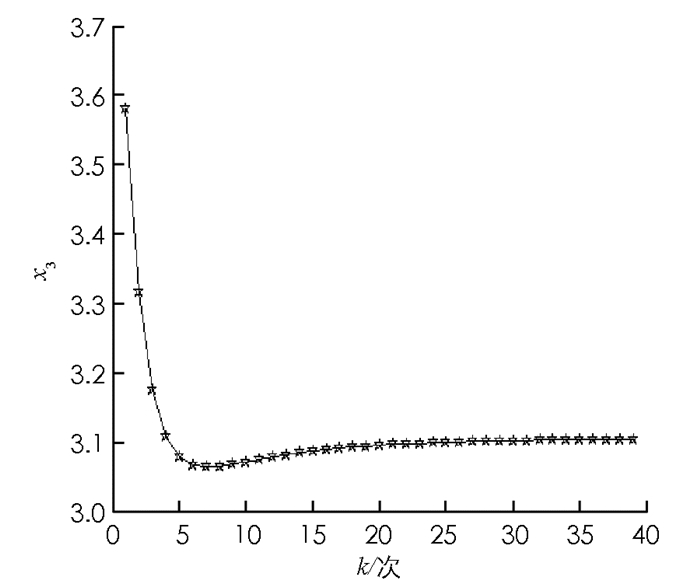
首先由(4)式计算三人合作对策的Shapley值为$\boldsymbol{\psi }\left( v \right) = {\left( {\begin{array}{*{20}{c}} {\frac{{14}}{3}, }&{\frac{{13}}{6}, }&{\frac{{19}}{6}} \end{array}} \right)^{\text{T}}} $.由于ψ₂+ψ₃ < v({2，3})，故Shapley值不在核心中，此时Shapley值的分配方式并不一定使每个局中人都满意，比如局中人2和3，因此合作将面临破裂的危险.易知该合作对策核心为C(v)={(4，3- x，3+ x)|0≤ x ≤2}，即核心存在但是不唯一，故无法通过核心的分配方式解决该问题.而最公平核心属于核心且满足唯一性、稳定性以及一定程度的公平性，因此求解合作对策的最公平核心是有必要的.下面通过matlab R2014a编码，在型号为270E4V的计算机上操作求解合作对策的最公平核心：根据本例的约束条件，将求解最公平核心转化为求解凸二次规划问题时可得：

计算时，相关参数取α=0.95， r=1.05，β=1.01，算法迭代的初始值记为 ω₀=(x₀，y₀，λ₀)^T，其中λ₀=(0，0，0，0)^T，y₀分别取值为(0，0，0，0)^T，(1，0，0，0)^T，(1，1，0，0)^T，(1，0，1，0)^T.下面以迭代次数k为横坐标，分别以局中人x₁，x₂，x₃所得为纵坐标，初始值取y₀=(1，1，0，0)^T时给出局中人在计算过程中迭代变化情况的图示(图 1-3).事实上，理论及数值实验表明，y₀在可行域内的任意取值并不影响局中人输出的最终结果.

从图 1-3也可以看出随着迭代次数的增加，各局中人所得值的变化趋于稳定，当迭代次数到达39次之后，各局中人所得近似值收敛到(4.000，2.899，3.101)^T.由于最公平核心属于核心，因此所得结果必定在核心的可行域内，由输出的局中人所得值也可得到这一点.比如核心中局中人2的所得分配范围为(1，3)，由于人工变量y最终仍要为0，所以局中人2所得分配有一些波动，但是最终变化趋势稳定，输出值约为2.899，这显然和核心中的分配一致.

为了更好说明本文算法的有效性，分别用本文算法以及INPSALM算法^[16]计算本例，计算结果见表 1.

由数据表 1可知，本文算法能够有效求解合作对策的最公平核心，与INPSALM算法相比，本文算法计算的迭代次数有所降低并且计算结果更加稳定，这一特点在局中人增多时更加有用，可以保证统一分配，避免纠纷，提高效率以及保证合作持续进行.

本文主要通过添加人工变量y将合作对策的最公平核心转化为凸二次规划问题，运用求解凸二次规划问题的带有正不定临界项的对称交替方向法(PIDSADMM)算法求解，可行域的简单闭凸性保证了算法收敛到最公平核心，同时也减少了算法的迭代次数，提高了收敛速度.简单的示例说明了该方法的可行性和有效性，为求解合作对策的解提供了新思路.但是本文算法依赖于参数的选择，这也是需要改进的部分.