Qualitative Analysis of Stochastic SIRI Model with Lévy Noise and Media Reports

近年来，各种传染病严重威胁着人类的健康，数学模型被认为是研究各种传染病动态的有力工具^[1-3].一些传染病暂时或永久免疫，用SIR，SIRS模型来描述；其他一些传染病，康复后的个体可能恢复成感染者，用SIRI模型来描述，如肺结核、疱疹^[4-5].最近，各种各样的数学模型都开始考虑媒体报道的影响.文献[5]提出下列带有媒体报道的随机SIRI模型：

其中：S(t)表示t时刻易感者的数量，I(t)表示t时刻感染者的数量，R(t)表示t时刻恢复者的数量；Λ表示单位时刻补充的数量，μ表示死亡率，α表示恢复率，γ为免疫失去率，Λ，μ，γ，α，λ，m都为正常数；β₁是媒体报道前的接触率，β₂是媒体报道后的接触率，由于报道不能完全阻止疾病的传播，所以β₁≥β₂＞0；B_i(t)表示有滤波${\left\{ {{\mathscr{F}_t}} \right\}_{t \ge 0}}$的完备概率空间(Ω，$\mathscr{F}$，${\left\{ {{\mathscr{F}_t}} \right\}_{t \ge 0}}$，$\mathbb{P}$)上的标准布朗运动；σ_i表示白噪声强度，i=1，2，3.

现实中，不仅传染病的传播会受到环境噪声的干扰，而且在传染病传播的过程中可能受到严重的环境扰动，如非典、洪水等.这些现象不可能用随机连续模型描述，进而引入Lévy跳来刻画这些现象.此外本文用更一般的函数(β₁-β₂f(I))SI来描述媒体报道的影响.

基于上面两点，在文献[6]的基础上，考虑带有Lévy噪声和媒体报道的随机SIRI模型：

其中：f(I)满足f′(I)≥0，f(0)=0，$\underset{I+\infty }{\mathop{\text{lim}}}\, \text{ }f\left(I \right)=1$；X(t-)表示X(t)在t处的左极限；N(dt，dy)是有平稳分布v(dy)dt的泊松计数过程且$\widetilde{N}$(dt，dy)=N(dt，dy)-v(dy)dt，${{\int }_{Y}}[\text{ln}(1+{{q}_{i}}\left(y \right))]v\left(\text{d}y \right)>-\infty $，${{\int }_{Y}}[{{q}_{i}}\left(y \right)-\text{ln}(1+{{q}_{i}}\left(y \right))]v\left(\text{d}y \right) < +\infty $，i=1，2，3；v定义在[0，∞)的可测子集Y上，且v(Y) < ∞；q_i是Y×Ω (-1，+∞)上的连续有界函数，i=1，2，3.模型(2)中其他参数的定义与模型(1)中相同.

定理1 对于任意初值(S(0)，I(0)，R(0))^T∈ $\mathbb{R}_{+}^{3}$，模型(2)存在唯一的全局正解(S(t)，I(t)，R(t))^T，即对任意t∈[0，∞)，(S(t)，I(t)，R(t))^T∈ $\mathbb{R}_{+}^{3}$a. s.

证 模型(2)的系数满足局部Lipschitz条件，对于任意的初值(S(0)，I(0)，R(0))^T∈ $\mathbb{R}_{+}^{3}$，模型(2)在区间[0， τ_e)存在唯一局部解x(t)=(S(t)，I(t)，R(t))^T，其中τ_e是爆破时刻.存在充分大的正整数k₀，使得S(0)，I(0)和R(0)都在区间$\left(\frac{1}{{{k}_{0}}}~, {{k}_{0}} \right)$内，对于所有的正整数k≥k₀，定义停时

此外，规定infØ=∞.显然{τ_k}是单调递增序列.设τ_∞=lim_{k +∞}τ_k.易知τ_∞≤τ_e.若能证明τ_∞=∞ a. s.则τ_e=∞ a. s.且(S(t)，I(t)，R(t))^T∈ $\mathbb{R}_{+}^{3}$ a. s.因此下面需证明τ_∞=∞ a. s.假设τ_∞ < ∞，则存在T∈(0，∞)和ε∈(0，1)，使得P(τ_∞≤T)>ε.

令$V(S, I, R)=\left(S-a-a\text{ln}\frac{S}{a} \right)+\left(I-1-\text{ln}I \right)+\left(R-1-\text{ln}R \right)$，其中a为待定正常数.由Itô公式^[6]得

其中

其中${{K}_{1}}={{\int }_{Y}}\left[a{{q}_{1}}\left(y \right)-a\text{ln}\left(1+{{q}_{1}}\left(y \right) \right) \right]v\left(\text{d}y \right)+$ ${{\int }_{Y}}\left[{{q}_{2}}\left(y \right)-\text{ln}\left(1+{{q}_{2}}\left(y \right) \right) \right]v\left(\text{d}y \right)+{{\int }_{Y}}\left[{{q}_{3}}\left(y \right)-\text{ln}\left(1+{{q}_{3}}\left(y \right) \right) \right]v(\text{d}y)$.取$a=\frac{\mu }{{{\beta }_{1}}}~$，则由(3)式得0≤EV(x(T∧τ_k))≤V(x(0))+KT.

令Ω_k={τ_k≤T}.当k≥ k₀时，P(Ω_k)>ε，并且有V(x(T∧τ_k))≥0.因此EV(x(T∧τ_k))≥E(1_ΩkV(x(T∧τ_k)))，其中1_Ωk是Ω_k的示性函数.对于任意ω∈Ω_k，由停时的定义，S(τ_k，ω)，I(τ_k，ω)，R(τ_k，ω)中至少有一个等于k或$\frac{\text{1}}{k}$，因此

所以V(x(0))+KT≥E(1_ΩkV(x(T∧τ_k)))P(Ω_k)=EV(x(τ_k，ω))P(Ω_k)≥A_kε，当k→∞时，有∞>V(x(0))+KT=∞，矛盾，故假设不成立，即τ_∞=∞ a. s.从而定理1得证.

模型(2)对应的确定性模型如下：

利用文献[8]中计算基本再生数的方法，易知模型(4)的基本再生数${{R}_{0}}=\frac{{{\beta }_{1}}\mathit{\Lambda }\left(\mu +\gamma \right)}{{{\mu }^{2}}\left(\mu +\gamma +\alpha \right)}~$.当R₀≤1时，模型(4)仅存在无病平衡点${{\mathrm{E}}_{0}}=\left(\frac{\mathit{\Lambda }}{\mu }, 0, 0 \right)~$；当R₀> 1时，模型(4)不仅存在无病平衡点${{\mathrm{E}}_{0}}=\left(\frac{\mathit{\Lambda }}{\mu }, 0, 0 \right)~$，还存在地方病平衡点E^*=(S^*，I^*，R^*).

定理2  如果R₀≤1，且$-\mu +{{\sigma }_{1}}^{2}+3{{\int }_{Y}}{{q}_{1}}^{2}\left(y \right)v\left(\text{d}y \right) < 0$，$-\mu +\frac{1}{2}{{\sigma }_{i}}^{2}+\frac{3}{2}{{\int }_{Y}}{{q}_{i}}^{2}\left(y \right)v\left(\text{d}y \right) < 0$，i=2，3，那么对于任意初值(S(0)，I(0)，R(0))^T∈ $\mathbb{R}_{+}^{3}$，模型(2)的解x(t)=(S(t)，I(t)，R(t))^T满足

其中$M=\{\text{min}~\mu -{{\sigma }_{1}}^{2}-3{{\int }_{Y}}{{q}_{1}}^{2}\left(y \right)v\left(\text{d}y \right)$，$\mu -\frac{1}{2}{{\sigma }_{2}}^{2}-\frac{3}{2}{{\int }_{Y}}{{q}_{2}}^{2}\left(y \right)v\left(\text{d}y \right)$，$\mu -\frac{1}{2}{{\sigma }_{3}}^{2}-\frac{3}{2}{{\int }_{Y}}{{q}_{3}}^{2}\left(y \right)v\left(\text{d}y \right)\text{ }\!\!\}\!\!\text{ }$，${{K}_{2}}={{\sigma }_{1}}^{2}~{{\left(\frac{\mathit{\Lambda }}{\mu } \right)}^{2}}+3{{\left(\frac{\mathit{\Lambda }}{\mu } \right)}^{2}}{{\int }_{Y}}{{q}_{1}}^{2}\left(y \right)v\left(\text{d}y \right)$.

证 令${{V}_{1}}\left(S, I, R \right)=\frac{1}{2}\left(S-\frac{\mathit{\Lambda }}{\mu }+I+R \right){{~}^{2}}+{{a}_{1}}I+{{a}_{2}}R$，其中a₁，a₂为待定正常数.由Itô公式^[6]得

其中

取${{a}_{1}}=\frac{2\mu }{{{\beta }_{1}}}$，${{a}_{2}}=\frac{2\mu \gamma }{{{\beta }_{1}}\left(\mu +\gamma \right)}~$，则

易知$0\le E{{V}_{1}}\left(x\left(t \right) \right)\le {{V}_{1}}\left(x\left(0 \right) \right)+E\int_{0}^{t}{~}\left(-M\left({{\left(S-\frac{\mathit{\Lambda }}{\mu } \right)}^{2}}+{{I}^{2}}+{{R}^{2}}+{{K}_{2}} \right) \right)\text{d}t$.从而

定理2得证.

记

定理3 如果R₀>1且A>0，B>0，C>0，那么对于任意初值(S(0)，I(0)，R(0))^T∈$\mathbb{R}_{+}^{3}$，模型(2)的解x(t)=(S(t)，I(t)，R(t))^T满足

证  令${{V}_{2}}\left(S, I, R \right)=\frac{1}{2}{{\left(S-{{S}^{*}}+I-{{I}^{*}}+R-{{R}^{*}} \right)}^{2}}+$ $\frac{p}{2}{{\left(S-{{S}^{*}}+I-{{I}^{*}} \right)}^{2}}+b\left(I-{{I}^{*}}-{{I}^{*}}\text{ln}~\frac{I}{{{I}^{*}}} \right)~+a\left(R-{{R}^{*}}-{{R}^{*}}\text{ln }\!\!~\!\!\text{ }\frac{R}{{{R}^{*}}} \right)$，其中a，b，p为待定正常数.由Itô公式^[6]得

其中

取$a=\frac{\gamma {{R}^{*}}}{\alpha {{I}^{*}}}$，$p=\frac{2\mu }{\gamma }$，$b=\frac{2\mu }{\gamma }\cdot \frac{\gamma +2\mu +\alpha }{{{\beta }_{1}}-{{\beta }_{2}}f\left({{I}^{*}} \right)~}$，则

易知$0\le E{{V}_{2}}\left(x\left(t \right) \right)\le {{V}_{2}}\left(x\left(0 \right) \right)+E\int_{0}^{t}{{}}\left(-N\left({{\left(S-{{S}^{*}} \right)}^{2}}+{{\left(I-{{I}^{*}} \right)}^{2}}+{{\left(R-{{R}^{*}} \right)}^{2}} \right)+{{K}_{3}} \right))\text{d}t$，从而

定理3得证.

注 在模型(2)中，令f(I)= $\frac{\mathit{I}}{\mathit{m}\text{+}\mathit{I}}$，q_i(y)=0，i=1，2，3，则模型(2)转化为模型(1).容易验证，定理2与3推广了文献[6]中的定理3.1与4.1.

本节利用Milsteins方法^[9-10]来验证本文主要理论结果.

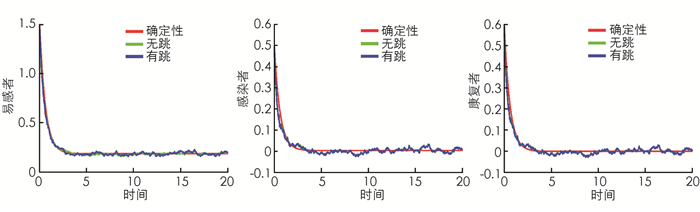
例1  对于模型(2)，在无病平衡点附近，令初值S(0)=1.5，I(0)=0.5，R(0)=0.6，Λ=0.3，β₁=0.005，β₂=0.003，μ=0.2，α=0.043，γ=0.033，σ₁=0.1，σ₂=0.1，σ₃=0.1，q₁(y)=q₂(y)=q₃(y)=0.25，v=0.8，易得R₀=0.04 < 1，且定理2的其他条件满足，因此定理2成立.如图 1所示.

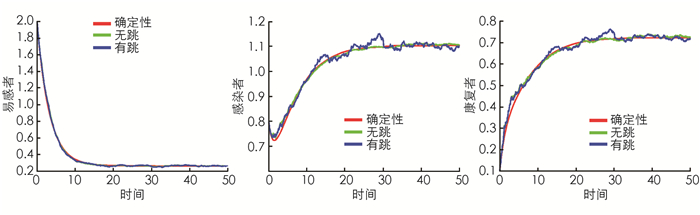
例2 对于模型(2)，在地方病平衡点附近，令初值S(0)=2，I(0)=0.8，R(0)=0.1，Λ=0.3，β₁=0.3，β₂=0.25，μ=0.15，α=0.285 7，γ=0.285 7，σ₁=0.02，σ₂=0.01，σ₃=0.02，q₁(y)=q₂(y)=q₃(y)=0.15，v=0.05，易得R₀=2.42>1，且定理3的其他条件满足，因此定理3成立.如图 2所示.