-
图的完美对集的计数问题的研究有重要的理论价值和现实意义[1-3].此问题已经被证实是NP-困难问题.分类嵌套递推的方法是求解许多类图完美对集数的一种非常有效的方法[4-10].本文构造了2类新的Nmn和3-nK3,3,用分类嵌套递推的方法求出了图Nmn和3-nK3,3不同完美对集的计数公式.
定义1 如果图G有1-正则生成子图P,那么就称这个生成子图P为图G的完美对集.
定义2 设图G是有完美对集的图,如果图G的两个完美对集P1和P2中有一条边不同,那么就称P1和P2是G的两个不同的完美对集.
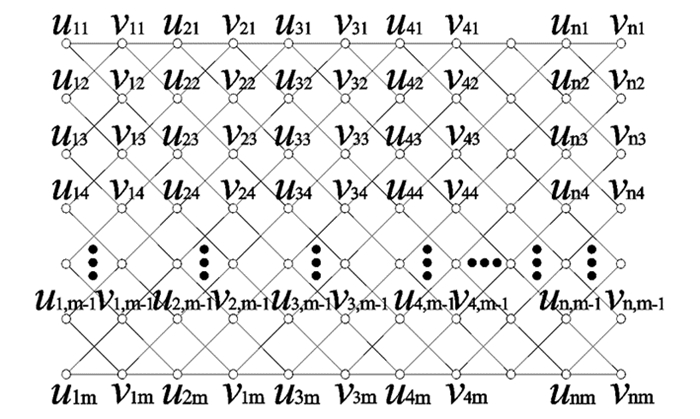
定义3 设长度为2m的圈Cmi的顶点集合为V(Cmi)={ui1,ui2,…,uim,vi1,vi2,…,vim}(i=1,2,…,n),把圈Cmi的顶点vi1,vi2,…,vim与圈Cmi+1的顶点ui+1,1,ui+1,2,…,ui+1,m(i=1,2,…,n-1)连接成圈vi1ui+1,2vi3ui+1,4vi5…vi,m-1ui+1,mvimui+1,m-1vi,m-2…ui+1,3vi2ui+1,1vi1(i=1,2,…,n-1),这样产生的图记为Nmn,见图 1.
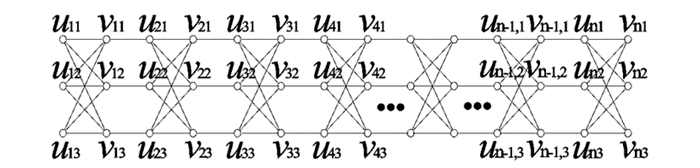
定义4 设完全偶图K3,3i的顶点集合为V(K3,3i)={ui1,ui2,ui3,vi1,vi2,vi3}(i=1,2,…,n),把圈K3,3i的顶点vi1,vi2,vi3分别与圈K3,3i+1的顶点ui+1,1,ui+1,2,ui+1,3 (i=1,2,…,n-1)各连接一条边,这样产生的图记为3-nK3,3,见图 2.
定理1 设图Nmn的完美对集数为δ(m,n),则δ(n)=2n.
证 因为图Nmn的每个圈Cmi:vi1ui2vi3ui4vi5…vi,m-1uimvimui,m-1vi,m-2…ui3vi2ui1vi1恰有2个完美对集(i=1,2,…,n),每个圈取定一个完美对集,就形成图Nmn的一个完美对集.因此,由乘法原理可知,图Nmn至少有2n个不同的完美对集.下面证明图Nmn只有2n个不同的完美对集.
设P是图Nmn的完美对集的集合,对于集合P中的任何一个完美匹配Pi,Pi一定要饱和顶点u11.与顶点u11关联的边只有2条,所以集合P可划分为2类:P1,P2.设u11v11∈P1,u11v12∈P2,则
$ P_{1} \cap P_{2}=\emptyset, P=P_{1} \cup P_{2}$ ,故δ(m,n)=|P|=|P1|+|P2|.因为u11v11∈P1,所以当m是偶数时,边u11v11,u12v13,v12u13,u14v15,v14u15,…,u1,m-2v1,m-1,v1,m-2u1,m-1,u1mv1m都属于P1; 当m是奇数时,边u11v11,u12v13,v12u13,u14v15,v14u15,…,u1,m-1v1m,v1,m-1u1m都属于P1.由δ(m,n)的定义可知,|P1|=δ(m,n-1).
因为u11v12∈P2,所以当m是偶数时,边v11u12,u13v14,v13u14,u15v16,v15u16,…,u1,m-2v1,m,v1,m-1u1,m都属于P2; 当m是奇数时,边v11u12,u13v14,v13u14,u15v16,v15u16,…,u1,m-2v1,m-1,v1,m-2u1,m-1,u1mv1m都属于P2.由δ(m,n)的定义可知,|P2|=δ(m,n-1).
因此,δ(m,n)=|P|=2δ(m,n-1)=…=2n-1δ(m,1)=2n.
定理2 设图 3-nK3,3的完美对集数为γ(n),则γ(n)=6n.
证 图 3-nK3,3存在完美对集是明显的.设图 3-nK3,3的完美对集的集合为S,对于集合S中的任何一个完美匹配Si,Si一定要饱和顶点u11.与顶点u11关联的边有3条,所以集合S可划分为3类:S1,S2,S3.设u11v11∈S1,u11v12∈S2,u11v13∈S3,则Si∩Sj=(1≤i < j≤3),S=S1∪S2∪S3.故γ(n)=|S|=|S1|+|S2|+|S3|.
S1划分为两类. S1中含边u11v11,u12v12,u13v13的完美对集集合记为S11; S1中含边u11v11,u12v13,v12u13的完美对集集合记为S12.由γ(n)的定义可知
因此,有
S2划分为两类. S2中含边u11v12,v11u12,u13v13的完美对集集合记为S21; S2中含边u11v12,v11u13,u12v13的完美对集集合记为S22.由γ(n)的定义可知
因此,有
S3划分为两类. S3中含边u11v13,v11u12,u13v12的完美对集集合记为S31; S3中含边u11v13,v11u13,u12v12的完美对集集合记为S32.由γ(n)的定义可知
因此,有
由(1)式和(2),(3)式,得
On Calculation Formula for Perfect Matching Number of Two Types of Graphs
- Received Date: 03/02/2020
- Available Online: 20/10/2020
-
Key words:
- classification /
- perfect matching /
- recurrence relation
Abstract: The perfect matchings of graphs Nmn and 3-nK3, 3 have been classified according to the edge associated with a vertex, and the recurrence relationship of the number of perfect matchings of each type been obtained, and then the sum and nested recursion methods been used to give the counting formulas for the different perfect matchings in graphs Nmn and 3-nK3, 3 are 2n and 6n.






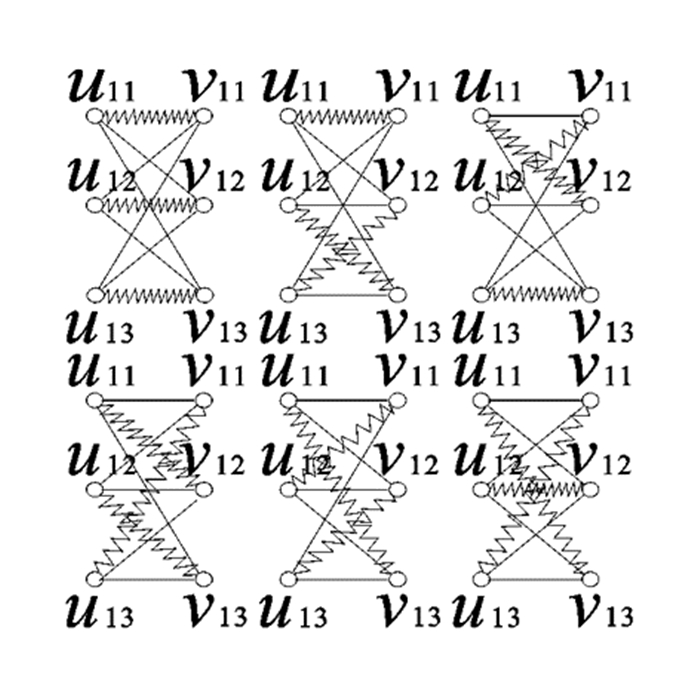
 DownLoad:
DownLoad: