-
开放科学(资源服务)标志码(OSID):

-
由于在工程实践中随机性广泛地存在于材料特性、外部荷载和边界条件等因素中,因此随机动力系统分析作为现代力学研究的重要分支,一直以来是人们研究的热点. 文献[1]从概率守恒的基本原理出发,发展了概率密度演化分析理论,建立了广义概率密度演化方程(GDEE),为复杂非线性随机动力系统的分析提供了一条可行的途径[2-4]. 已有的工作证明:这一新的分析理论在线性与非线性系统的随机动力反应分析[5]、结构动力可靠度计算[6-7]、结构随机最优控制等[8]方面均可获得高效、准确的分析结果.
广义概率密度演化方程作为一类偏微分方程,近年来众多学者发展了一系列解析和半解析的求解方法[9-10]对其进行求解. 本文从随机动力系统的相空间出发,提出了一种可用于精确、高效求解非线性系统的GDEE求解方法——相空间重构法(PSRM). 本文利用该方法,得到了若干典型非线性振子的概率密度解,并将其与Monte Carlo模拟方法[11]、有限差分法[9]等数值求解方法进行了比较,验证了该方法的准确性、有效性和便捷性.
全文HTML
-
文献[5]发展了一类用于随机系统分析的广义概率密度演化方程,经过十数年的发展,这一方法广泛地应用于结构的可靠性分析[5]、铁路轨道设计[12]以及城市基础设施防震减灾设计[13-14]等领域之中.
不失一般性,设随机动力系统为
初始条件为
其中:X0=(X1,X2,…,Xn)T,n是物理系统的维数;G(·)为一般非线性系统,Θ=(Θ1,Θ2,…,Θs)T,其联合概率密度函数为pΘ(θ),s是系统中随机变量的总数. 显然,对于特定的随机动力系统,方程(1),(2)的解存在且唯一,并连续地依赖于初始条件. 即对于给定的初始条件,式(1)的解可写为
初始条件为
由于广义密度演化方程的解析解很难得到,工程中常用其数值解.
-
在大多数非线性问题乃至工程问题中,式(4)和式(5)的解析求解都是相当困难的. 由此,大量学者发展了一系列数值和近似的解析算法用于求解广义概率密度演化方程[16-17]. 本文通过深入研究广义概率密度演化理论的物理机制,在此基础上提出了一类基于非线性物理系统分解的相空间重构方法,可以有效避免采用传统点演化方法求解广义概率密度演化方程时所遇到的网格敏感性问题和数值耗散问题.
不妨令
则方程(6)可化为
当a≠0时,存在
对一般的情况而言,关于g(x)的δ函数已在文献[20]中给出
其中xi是g(x)的一个根. 将式(10)代入式(8)的形式解可得到
其中
$\widetilde{\boldsymbol{\theta}}_{i}$ (x,t)是G(θ,x,t)=0的根线,Nsol是G(θ,x,t)=0根线的个数. 利用狄拉克δ函数的基本性质[21]联立式(8),(11)和(12),对θ求积分可得
其中:Heaviside(·)是赫维赛德函数[22],Ω(Θi)是积分区域. 由式(13)可知,非线性系统可以由相空间X-θ物理系统G(θ,x,t)中的数个物理系统
$\widetilde{\boldsymbol{\theta}}_{i}$ (x,t)组合而成. 对应地,也可以在代数上理解函数G(θ,x,t)可以被分解为若干个值域不重合的单调函数$\widetilde{\boldsymbol{\theta}}_{i}$ (x,t)的叠加.因此,在相空间X-θ的角度处理广义概率密度演化方程(GDEE)的求解问题避免了反函数求解这一数学上的难点;同时,由于在实际中我们往往主要关注一个物理量(如位移)或是两个物理量(位移和速度)的概率密度函数,这也大大简化了X-θ空间中的G(θ,x,t)曲线,使得对物理系统G(θ,x,t)的分解成为可能.
基于物理系统分解的数值求解方法步骤如下:
1) 在随机变量Θ的分布空间ΩΘ任意选取一定量的离散点Θ=θq,q=1,2,…,Nsol,求解物理方程,提取t时刻的所需物理量xq(θq),同时计算t时刻所需物理量的时间导数ẍq(θq);
2) 对X-θ空间中的物理系统进行分类,将分布空间ΩΘ分为ΩΘ1,ΩΘ2,…,ΩΘNcla;Ncla为物理系统的分类个数;
3) 在不同的分布空间ΩΘNcla中,将X-θ空间中的离散点(θq,xq(θq))和(θq,ẋq(θq))代入式(13)中,得到不同分布空间ΩΘNcla下对应的概率密度函数的离散点集(xq(θq),pX(xq(θq)))ΩΘNcla;
4) 对各个分布空间ΩΘ中的概率密度函数点集(xq(θq),pX(xq(θq)))ΩΘNcla进行函数拟合,得到对应的pX(x(
$\widetilde{\boldsymbol{\theta}}_{g}$ (x)));5) 将所有的pX(x(
$\widetilde{\boldsymbol{\theta}}_{g}$ (x)))叠加,得到所求物理量的概率密度函数pX(x)=$\sum\limits_{g=1}^{N_{\text {cla }}}$ pX(x($\widetilde{\boldsymbol{\theta}}_{g}$ (x))).
-
单自由度振子(Single Degree of Freedom Oscillator)的无阻尼自由振动是一种简谐振动,其固有频率是系统本身的性质,与初始条件无关,且它的速度与加速度也是简谐的. 其方程可以写为
其初始条件为
随机变量ω在区间[0.1,0.4]内均匀分布,由于该方程为线性微分方程,其解析解易得为
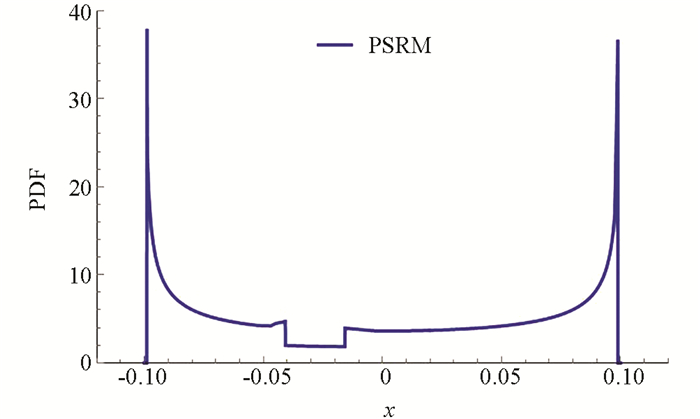
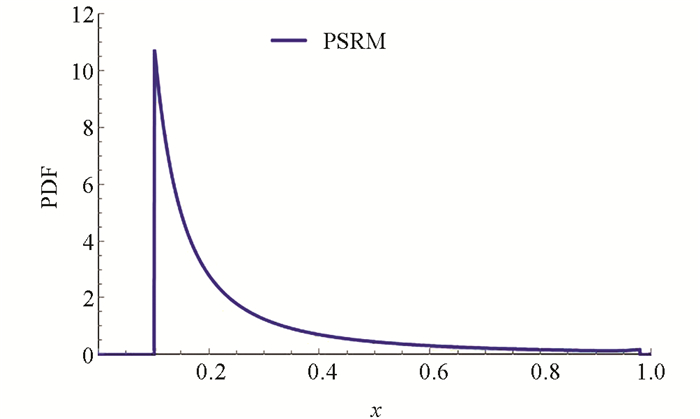
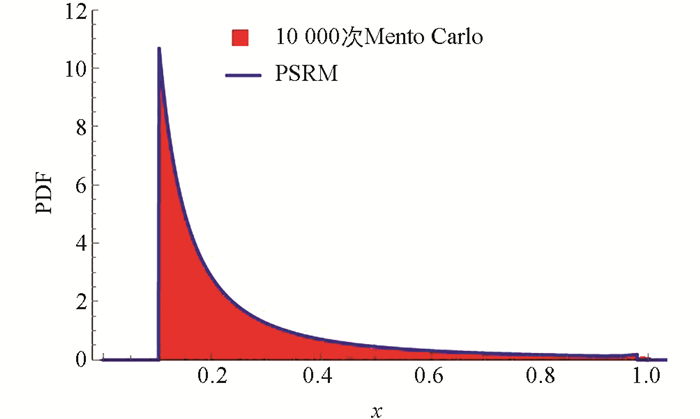
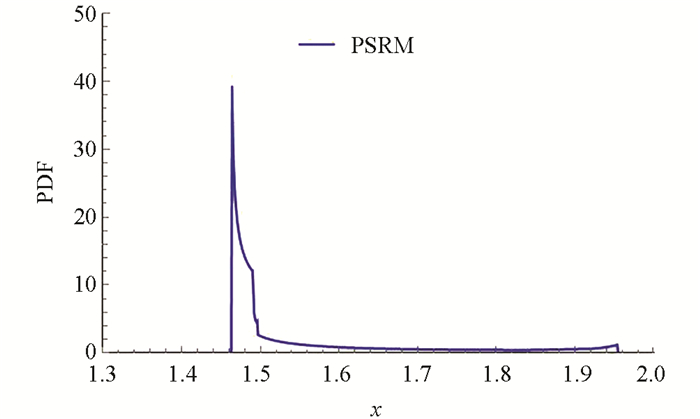
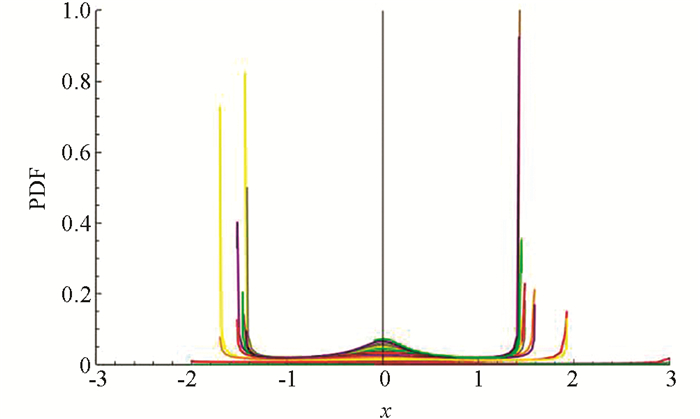
图 1为使用PSRM分解物理系统后的各个概率密度函数,将各物理系统的概率密度函数叠加得到图 2.
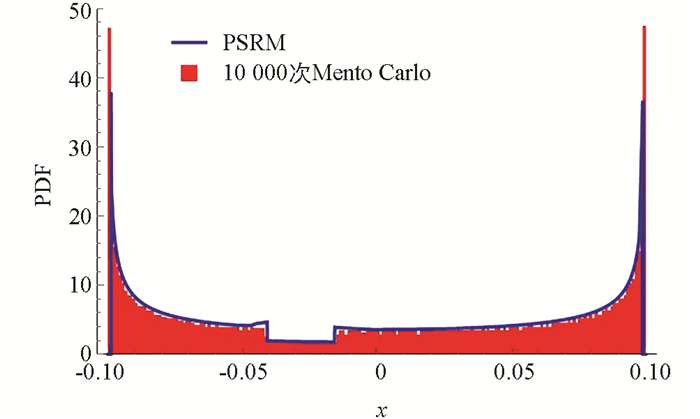
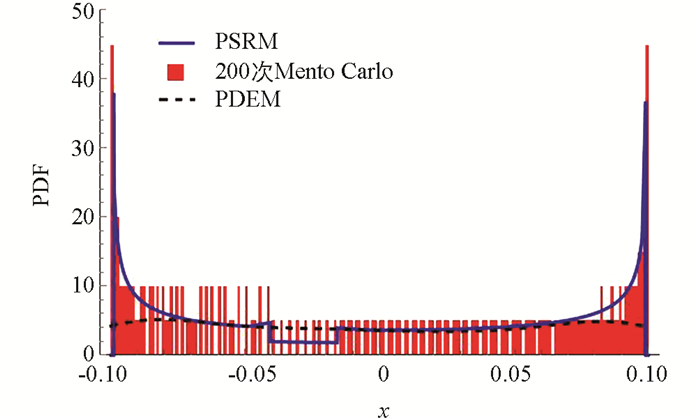
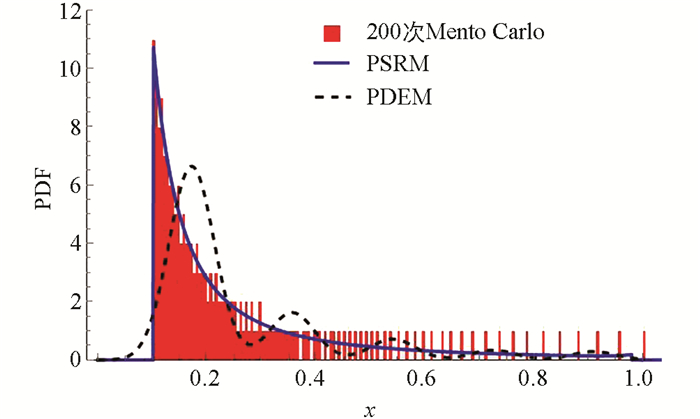
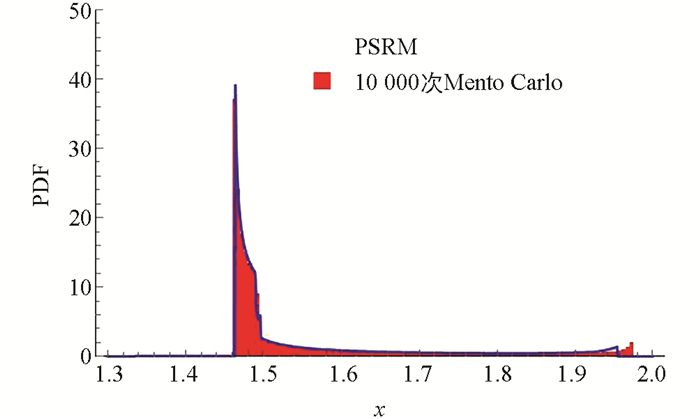
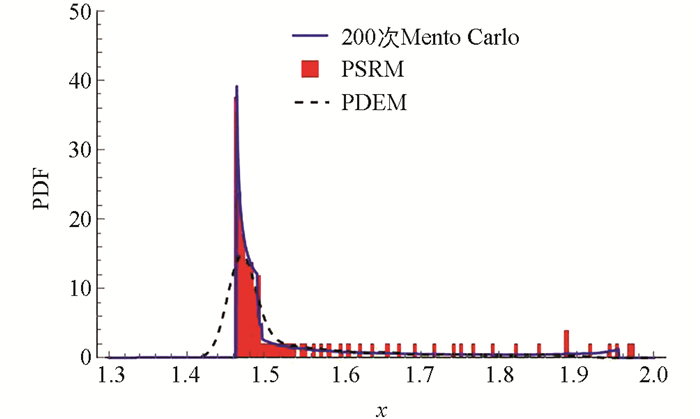
通过10 000次Monte Carlo模拟与本文提出的相空间重构法进行比较(图 3),可以看出本文所提出的PSRM与精确解的吻合程度较好. 图 4给出了代表点个数相同(200个)的情况下,使用Monte Carlo模拟方法、PDEM和PSRM在典型时刻(t=20)响应的概率密度函数. 由表 1失效概率数据可以看出,相比传统的PDEM,PSRM使用较少的代表点个数即可获得较高的计算精度.
-
Riccati振子是控制理论中的重要方程,涉及Kalman滤波、信号频率跟踪[23]、线性二次调节器问题及模型简化等诸多问题[24-25]. 设一阶Riccati方程为
其初始条件为
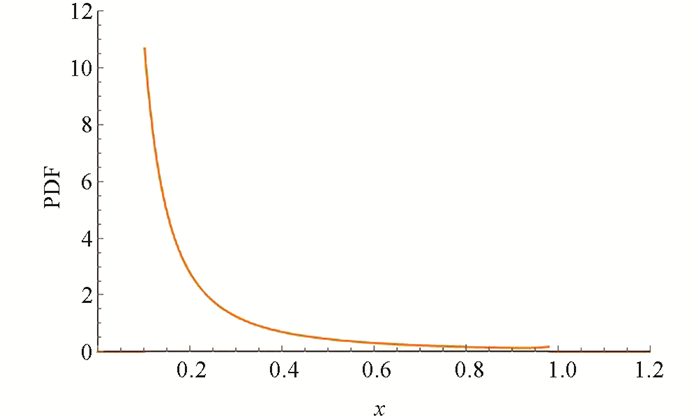
图 5为使用PSRM分解Riccati振子得到的概率密度函数,叠加概率密度函数得到图 6.
随机变量θ在区间[1, 10]均匀分布. 用10 000次Monte Carlo模拟与本文提出的相空间重构法进行比较(图 7),可以看出本文所提出的PSRM与精确解的吻合程度较好. 图 8给出了代表点个数相同(200个)的情况下,使用Monte Carlo模拟、有限差分方法PDEM和PSRM在典型时刻(t=20)响应的概率密度函数. 由表 2失效概率数据可以看出,相比传统的PDEM,PSRM使用较少的代表点个数即可获得较高的计算精度.
-
Van der Pol振子是非线性系统的经典模型之一,它起源于范德波尔对电子电路中三极管的振荡效应的研究[26]. 这一模型在物理学、生物学、神经学甚至经济学中,都有着广泛的应用[27-28]. 设一维Van der Pol方程为
初始条件为
使用PSRM分解Van der pol振子的物理系统(图 9),叠加各个物理系统的概率密度函数得到图 10.
随机变量θ在区间[0.1,5]均匀分布. 用104次Monte Carlo模拟与本文提出的相空间重构法进行比较(图 11),可以看出,本文所提出的PSRM与精确解的吻合程度较好. 图 12给出了代表点个数相同(200个)的情况下,使用Monte Carlo模拟、PDEM和PSRM在典型时刻(t=20)响应的概率密度函数. 由表 3失效概率数据可以看出,相比传统的PDEM,PSRM使用较少的代表点个数即可获得较高的计算精度.
-
Duffing振子是一个典型的非线性振动系统,尽管是从简单物理模型中得出来的非线性振动模型,但是其模型具有代表性. 工程实际中的许多非线性振动问题的数学模型都可以转化为该方程来研究,如脑电识别[29]、机械臂振动控制[30]、微弱信号检测[31]等,Duffing系统也非常广泛地被应用到实际工程中,例如尖锐碰摩转子的故障检测、微弱周期信号检测、电力系统周期振荡分析、周期电路系统的模拟与控制等[32-34]. 设一维Duffing方程为
初始条件为
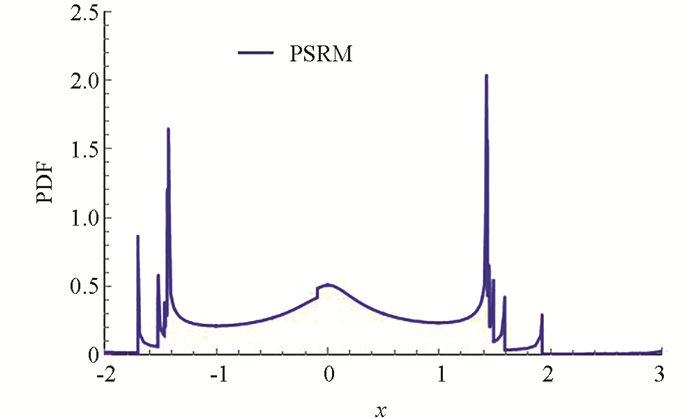
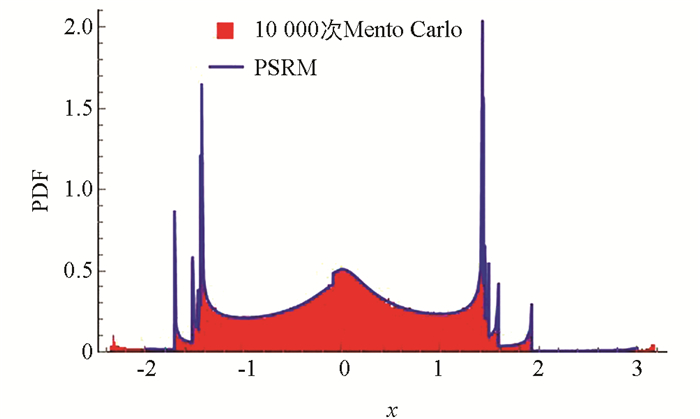
用PSRM分解Duffing振子的14个物理系统,得到各物理系统的概率密度函数(图 13),并叠加各系统的概率密度函数(图 14).
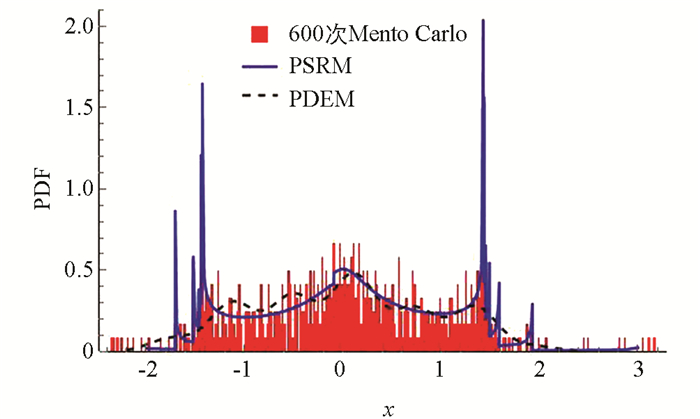
随机变量a在区间[0.1,5]均匀分布. 用Monte Carlo模拟与本文提出的相空间重构法进行比较(图 15),可以看出本文所提出的PSRM与精确解的吻合程度较好. 图 16给出了代表点个数相同(600个)的情况下,使用Monte Carlo模拟、PDEM和PSRM在典型时刻(t=20)响应的概率密度函数. 由表 4失效概率数据可以看出,相比传统的PDEM,PSRM使用较少的代表点个数即可获得较高的计算精度.
3.1. SDOF振子
3.2. Riccati振子
3.3. Van der Pol振子
3.4. Duffing振子
-
广义概率密度演化方程作为求解随机动力系统的一种通用方法,近年来获得了广泛的关注. 传统的广义概率密度演化方程数值算法,往往需要提前对概率空间进行剖分,通过获取广义概率密度演化方法的点演化方程来求解. 本文通过深入研究广义概率密度演化理论的物理机制,对代表物理系统的相轨迹进行分解,然后对分解后的广义概率密度演化方程分别进行求解,叠加后即可得到原非线性系统的概率密度解. 相比于传统的数值求解方法,本方法不需要求解代表点的赋得概率,且所需的代表点个数较少. 最后,通过4个数值算例,证明了该方法可以有效地计算强非线性系统随机响应.
本文结果不仅可以作为求解广义概率密度演化方程的一种半解析方法,同时也证明了广义概率密度演化方程既可以从概率空间剖分角度进行求解,也可以从物理系统分解角度进行求解,有助于进一步深入研究和剖析随机动力系统中随机性与非线性的耦合机制.



 下载:
下载: