-
无监督学习[1]是机器学习中的一项重要技术,其中聚类分析与应用[2-30]在近年来得到了广泛关注.
传统的聚类方法大致可以分为:基于划分的聚类算法[9-12]、基于模糊理论的聚类算法[16-20]、基于密度的聚类算法[21-23]等.除此之外,受传统聚类算法的启发,为完成更广泛的任务,越来越多的新颖的聚类算法被提出[24-30].但以上算法在解决超多类聚类问题时却并不理想[31-33].
文献[34]提出了空间结构表示框架,可有效应对符号型数据空间结构模糊的问题,并应用于符号数据聚类问题中[35-36].基于空间结构的表示方法将原始符号型数据映射到一个概率表示空间,在保持原有类结构信息的前提下,该方法提供了更加丰富的测度信息,从而使原始符号数据的类结构信息更加清晰.借助该思想,本文提出了一种多角度空间结构的数据聚类算法,从多个角度构建数据的空间结构,以期更全面地识别数据空间中存在的类结构,从而应对多类簇数据聚类问题.该方法利用特征抽样从多个视角刻画原始数据集,然后构建不同视角下的空间结构表示,再集成这些不同视角下的数据表示得到一个统一的表示矩阵,最后利用该矩阵完成聚类.
本文的主要贡献包括3个方面:
1) 多角度空间结构表示方法.本文提出了一种从多个角度对原始数据集进行空间结构表示的方法,以更加准确地识别复杂的类簇分布结构;
2) 多角度空间结构聚类方法.本文提出多角度空间结构聚类算法框架,集成多个视角所形成的空间结构来对数据进行更有效地聚类;
3) 本文在10个真实数据集上验证了多角度空间结构聚类算法相较于传统聚类算法的优越性.
HTML
-
本章内容将分别介绍符号型数据和数值型数据的空间结构表示方法.
-
符号型数据是由一组有限和无序的特征向量来表示,所以无法像数值型数据那样直接度量样本间的相似度或距离,且难以准确刻画符号型数据的空间分布结构,这导致许多聚类算法无法处理符号型数据.
为更清晰地刻画符号型数据的空间结构,文献[34]基于样本间相似性概率提出了一种空间结构表示方法,具体如下:
假设U={x1,x2,…,xn}为数据集合,A={a1,a2,…,am}为特征集合,如果A中的特征均为符号型特征,则数据集U为符号型数据集.
假设T=(U,A)为符号数据集,其中U为样本集,A为属性集,表 1给出了一个表示示例.
样本xi和样本xj的相似性概率为:
其中:αl(x)为数据x的第l个特征值,
通过计算两两样本间的相似性概率,可得到符号型数据的空间结构表示矩阵为:SC=[pij]n×n,在符号型数据的空间结构中,一个样本的特征为{bi=xi,1≤i≤n},表 2给出了符号型数据的空间表示示例.
空间结构表示矩阵可以将符号型数据映射到一个欧式空间.
-
虽然空间结构表示方法最初是针对符号型数据提出,但该方法很容易扩展至处理数值型数据任务.
对于数值型特征al,样本xi和样本xj相似的概率为:
其中
$ \max \left( {{\boldsymbol{a}_l}} \right) = \mathop {\max }\limits_{1 \le i \le n} \left\{ {{\boldsymbol{a}_l}\left( {{\boldsymbol{x}_i}} \right)} \right\}, \min \left( {{\boldsymbol{a}_l}} \right) = \mathop {\min }\limits_{1 \le i \le n} \left\{ {{\boldsymbol{a}_l}\left( {{\boldsymbol{a}_i}} \right)} \right\} $ .基于公式(3),样本xi和样本xj相似的概率为:通过计算两两样本间的相似性概率,可得到数值型数据的空间结构表示矩阵为SN=[pij]n×n.
本文借助上述空间结构表示方法的思想,提出了一种多角度空间结构聚类算法,通过从多个角度构建原始数据集的空间结构,使得类簇结构信息更加清晰准确,进而解决数值型数据的超多类聚类问题.
1.1. 符号型数据的空间结构表示方法
1.2. 数值型数据的空间结构表示方法
-
为从多个角度刻画原始数据集,本文采用装袋(Bagging)算法.装袋算法被广泛地应用于监督学习任务中,通过有放回地抽样数据集,训练多个模型,这样可以降低模型泛化误差,其采用的策略为模型平均,即使用训练好的若干学习器来对新的未知样本预测.这种算法是一种集成方法,通过集成多个弱学习器来提高模型的学习性能.
在这种集成思想的启发下,本文通过对原始数据集的特征进行有放回地抽样,以从多个不同的视角来刻画原始数据.这样可以从不同的角度来描述一个样本,以期为后续揭示更清晰的类簇分布信息奠定基础.令U={x1,x2,…,xn}为数据集合,A={a1,a2,…,am}为特征集合,通过对特征集A进行有放回采样可得到新视角下的特征集描述B={b1,b2,…,bm}以及新视角下的数据集合U′={x1′,x2′,…,xn′}.
本文所提算法每次随机有放回地抽取与原始数据集相同维数的特征,形成新视角下的数据集.为进一步提升特征对原始数据结构的表达能力,本文在每次特征抽取完成之后,均对新的数据进行特征提取.另外,当原始数据集的特征较多时,每次形成的数据也具有较高的维度,会导致存储空间的浪费以及降低计算效率.因此,特征提取在减少存储空间的同时提高了计算效率.
本文所提算法采用PCA降维技术来对数据集进行降维处理.PCA是一种被广泛使用的数据降维算法.其主要思想是将数据从n维输入空间映射到k维特征空间.即将每个n维数据点通过映射转换成另一个数据点.其工作原理是,从原始数据空间中依次找出相互正交的坐标方向.第一个坐标方向选择数据集中方差最大的维度所在的方向,第二个坐标方向选择与第一个方向呈正交的平面中与方差最大的坐标方向,第三个坐标方向选择与前两个坐标方向呈正交的平面中方差最大的坐标方向,依次类推.最后会发现大部分数据基本集中在k个坐标方向中,所以后面的坐标方向可直接忽略,从而达到降维目的.对于数据矩阵Un×d′,PCA降维流程如下:
1) 求Un×d′的协方差矩阵Cn×n=COV(U′);
2) 求解协方差矩阵的特征值和特征向量;
3) 选取最大的k个特征值所对应的特征向量组成的矩阵Pd×k;
4) 计算Bn×k=Xn×dPd×k;
将B视为一个视角下的数据集.通过多次对特征的重抽样和提取,可得到多个视角下的数据集描述.
-
为了可以提供更清晰的类簇分布结构信息,本文结合数据的空间结构表示和多角度表示提出一种多角度空间结构表示方法.
样本间距离度量可以反应更加精细的结构信息,由此本文通过集成多个视角下的空间结构度量信息来构建统一地、更精细的数据表示,同时将多角度数据映射到同一个欧式空间中,便于之后的聚类分析.
首先,定义一个单一视角下的数据空间结构表示矩阵:
假设
$ B' = \left\{ {{{\boldsymbol{x}'}_1}, {{\boldsymbol{x}'}_2}, \cdots , {{\boldsymbol{x}'}_n}} \right\} $ 为第t个视角下的数据集合,基于公式(1)可求得B′的空间结构表示$ \boldsymbol{S}' = {\left[ {{{s'}_{ij}}} \right]_{n \times n}} $ ,其中$ {s'_{ij}} = p\left( {{{\boldsymbol{x}'}_i}, {{\boldsymbol{x}'}_j}} \right) $ .由空间结构的构造方法易知,空间结构表示的数据由规范化的特征描述,数据存在于第一象限,且取值范围区间为[0, 1].另外,一个数据在多个视角下的空间结构表示的特征维数相同,均为样本个数n.因此,可通过对应位置求平均的方法对一个数据的多个空间结构表示进行融合,即:
至此完成了原始数据的多角度空间结构的表示.
2.1. 多角度数据表示
2.2. 多角度空间结构融合
-
基于数据的多角度空间结构表示方法,提出了一个多角度空间结构聚类算法MS2BC(multi-viewspacestructure-basedclustering).该方法一方面借助了空间结构表示方法在数据类结构清晰化上的优势,另一方面从多个角度刻画数据的空间结构.因此,当类簇数量增多时,该方法有望缓解直接在原始数据上聚类难以识别类簇结构的问题,进而提升聚类性能.具体步骤如下:
1) 对特征进行与原始特征空间维数相等的装袋算法抽样,得到映射到多个视角的数据集合;
2) 对每个视角下的数据集合进行空间结构表示,再集成所有的结构表示信息;
3) 对集成后的空间结构表示进行聚类,获得数据集合的类簇划分结果.
对于步骤3),可以采用不同的聚类方法对空间结构表示进行聚类.本文采用的是谱聚类算法.
本小节给出本文所提算法的整体算法流程,伪代码描述如下:
算法整体分为2个阶段:第一阶段是构造多视角空间结构表示;第二阶段基于该空间结构表示聚类.从算法框架可以看出,本文算法在第一阶段构造多视角空间结构表示时,循环m次,每轮循环将执行特征装袋算法、PCA降维以及构建空间结构表示矩阵,其中构建空间结构表示矩阵的时间复杂度为O(n2).因此,算法第一阶段的时间复杂度为O(m(d+O(PCA)+n2)),其中m表示循环次数,d表示数据维数,n代表样本个数.算法的第二阶段利用谱聚类对第一阶段得到的空间结构表示进行聚类.因此第二阶段的时间复杂度为O(SC).综上所述,本文所提的算法的时间复杂度为O(m(d+O(PCA))+n2+O(SC)).
此外,本文所提算法可并行性较强,且易扩展至处理大规模数据.首先,多角度构建空间结构部分具有天然的可并行性,不同视角下构建空间结构可分布式运行;其次,在构造空间结构时可选取具有代表性的样本进行度量,构造空间结构表示矩阵S[n×n′](其中n′<n为代表性样本数),从而提升该部分的运行速率;最后,算法第二阶段所采用的谱聚类可借鉴现有快速算法来加速聚类过程,如U-SPEC[37].
-
为验证MS2BC算法的有效性,本文对比该方法与6个代表性聚类算法在10组真实数据上的聚类性能.
-
本文实验部分采用10个数据集,数据集的详细信息如表 3所示.其中glass,solar,zoo以及segment等4个数据集类簇较少,lsolet,ORL,corel_5k,Mpeg7,caltech101和Tdt2等6个数据集类簇较多.
-
调整兰德指数(adjustedrandindex,ARI)和标准互信息(normalizedmutualinformation,NMI)是评价聚类算法好坏的两个常用指标,被广泛使用,两者均为外部指标.
NMI值定义如下:
其中:P,Q为两种聚类结果;I(·)为其互信息;H(·)为信息熵.
ARI值定义如下:
其中:nij表示在分类结果X,Y中,Xi类与Yj类相同的对象个数;bi表示Xi类的对象个数;dj表示Yj类的对象个数.
两者取值在0~1之间,聚类结果越接近数据集的真实分布,NMI和ARI指标越高.本文采用以上两个指标衡量所提算法的有效性.
-
本文采用的对比方法包括K-means、AP、HC、谱聚类(SC)、U-SPEC[37]以及AD-AP[38]等6种方法.表 4列出了7种方法的NMI值,表 5列出了7种方法的ARI值,其中粗体表示每个数据集上评价指标取得的最高值.
从表 4可以看出本文所提算法在8个数据集上的NMI值达到了最高,其中在zoo,lsolet,ORL等3个数据集上NMI值均达到了0.75以上,说明本文所提算法的聚类性能优于其它算法.另外,在数据集caltech101上,传统聚类算法的NMI值较低,但本文所提算法确取得了不错的聚类结果.从表 5可以看出本文所提算法在8个数据集上ARI值达到了最高,本文所提算法的聚类性能优于其它算法.另外,在数据集ORL上,传统聚类算法的ARI值较低,但本文所提算法确取得了不错的聚类结果.本文所提算法在8个数据集上两个指标均达到了最高.
上述分析表明我们的算法相比于传统聚类算法具有竞争优势,同时也反映出我们的算法的确克服了传统聚类算法在类簇数量增多时聚类性能下降的问题.
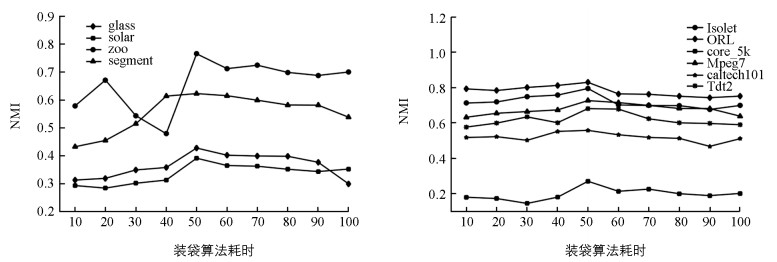
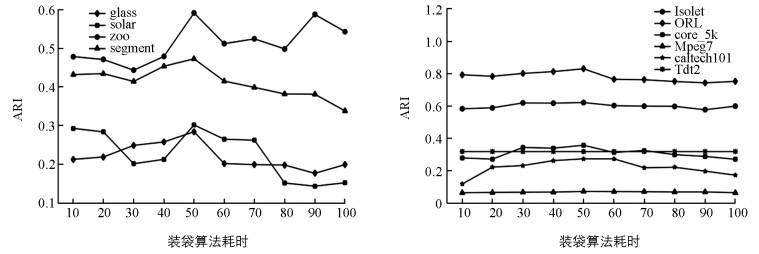
图 1和图 2分别表现了在不同数据集上,NMI和ARI随特征抽取次数的增大所发生的变化.从图中可以清晰看到本文算法较为平稳,且这些折线也反应出当特征抽取次数较小时,聚类性能随抽取次数的增大而增大;当特征抽取次数较大时,聚类性能随抽取次数的增大而下降.关于如何根据具体规模的数据集选择合适的特征抽取次数将作为本文未来研究工作.
4.1. 数据集描述
4.2. 评价指标
4.3. 实验结果及其分析
-
大数据背景下的聚类任务中,类簇数量剧增,给传统聚类方法带来了巨大挑战.针对该问题,本文提出了一种多角度空间结构聚类算法,通过集成数据的多个视角空间结构来加强算法识别类簇的能力,进而提升聚类性能.从实验结果的对比中可以看出,相较于传统聚类算法,本文所提算法取得了较高性能指标.未来我们重点研究本文所提算法的快速算法和并行算法,从而有效应对大规模超多类数据的聚类问题.






 DownLoad:
DownLoad: