-
开放科学(资源服务)标识码(OSID):

-
柑橘是我国南方地区栽培面积最广、经济价值最显著的水果之一,也是全球最重要的果树作物之一[1]. 南方柑橘果园主要分布于丘陵和山地地区,果园地形复杂,坡度较大,且机械化程度较低. 为了提高果园生产效率和增加种植收益,推动果园作业机械向自动化和智能化发展已势在必行[2]. 因此,果园作业机械的自主导航技术成为农业移动机器人研究的一个重要组成部分[3].
机器人自主导航能够根据周围环境信息规划最优路径,并控制自身行走机构沿着最优路径行驶. 目前广泛使用的导航传感器有全球导航卫星系统(Global Navigation Satellite System,GNSS)、惯性测量单元(Inertial Measurement Unit,IMU)、视觉相机、激光雷达等[4]. 魏爽等[5]使用GNSS系统定位,根据用户设置生成预设路径,建立基于预瞄点搜索的纯追踪模型,并将该模型用于农机转向控制,从而实现农机的自主导航. GNSS系统能在空旷的环境中展现出其优越性和巨大的潜力,但在果园环境中,果树的树冠和枝杈较密,GNSS系统由于遮挡无法稳定接收卫星信号,容易造成机器人丢失行进目标和自身定位信息,难以单独应用于果园环境.
随着机器视觉技术的发展,图像处理方法变得更加丰富,处理难度降低,同时相较激光雷达和GNSS系统,摄像头成本更低,所以近年来国内外有许多学者利用机器视觉技术来进行导航的研发与设计. 赖汉荣等[6]使用单目相机获取玉米苗带图像,经过图像处理后,利用最小二乘法拟合出玉米苗带,从而根据机器人航向与玉米苗带偏差实时调整导航线,实现玉米除草机器人的自主作业. 张振乾等[7]利用双目相机获取机器人前方场景点云,对点云处理后进行二维投影,然后采用改进K-means算法分离两侧香蕉树,从而进行导航线的提取. Ball等[8]设计了一款名为AgBot的机器人,通过双目相机和GNSS系统感知周围环境及自身定位,并利用ROS系统的move_base功能包实现大面积开阔农田环境下农业果园机器人的自主作业.
在开阔、平整的农田中,以上研究在准确性、鲁棒性、适应性方面均展现出良好效果,能够满足农田作业需求. 但是在丘陵山地,GNSS系统信号丢失严重,无法使用卫星定位. 果园地形高低起伏,导致地图构建难度增加,并且地形复杂,坡度变化较大,容易出现打滑及侧倾现象,增加了机器人自身控制的难度. 为应对该挑战,本文提出了一种基于激光雷达(Light Detection and Ranging,LiDAR)和惯性传感器(Inertial Measurement Unit,IMU)的丘陵山地柑橘果园机器人自主导航系统,该系统能感知周围环境的起伏变化和机器人自身姿态的改变,以自校正PID控制器精确控制机器人在果园复杂环境下的运动. 首先利用SLAM(Simultaneous Localization and Mapping)算法融合激光雷达和惯性传感器信息,构建果园三维点云全局地图;然后通过去除地面点云,获取安全行驶区域,使用多约束规划算法选取从起始点到目标点的最优路径;最后应用NDT-ICP算法进行局部点云和全局点云地图匹配,获取当前时刻机器人在全局地图中的位姿,从而实现机器人在果园中的路径规划与导航.
全文HTML
-
西南地区机械化柑橘果园主要分布在丘陵山地,柑橘果树株间距约为2.5~3 m,果树高度约为2 m,冠层直径约为1.5~2 m,柑橘果树行间距一般选用3.5~4.5 m,果园内作业道路宽度约为2 m[9].
本研究机器人自主导航作业果园位于四川省广安市武胜县(30.35369411°N,106.19301414°E),果园种植面积约为6.67 hm2,果树株间距约为3 m,行间距约为4 m,果园最大坡度约为25°. 柑橘果园树行实物如图 1所示.
-
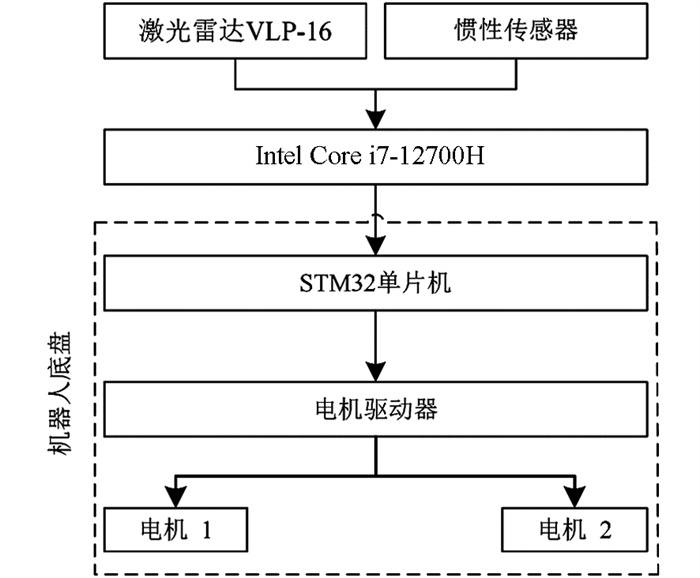
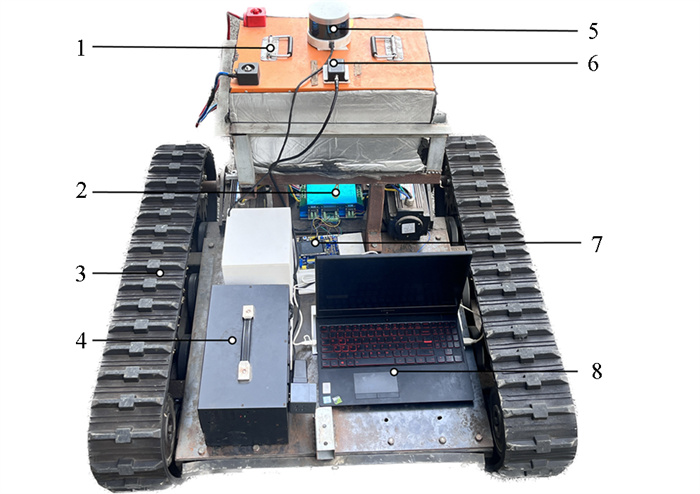
图 2为柑橘果园机器人硬件组成,该机器人选用16线激光雷达Velodyne VLP-16,其最大测距为100 m,精度为±3 cm,垂直视野为30°(±15°),水平视野为360°,垂直角分辨率为2°,水平角分辨率根据旋转速率不同从0.1°到0.4°不等. 在试验中,激光雷达的扫描速率设定为10 Hz,水平角分辨率为0.2°,通过100 Mbps以太网与主控单元通信. 主控单元为搭载Intel Core i7-12700H的笔记本电脑,预装Ubuntu 18.04系统. 底盘采用履带式底盘,履带由2个1.5 kW的直流无刷电机驱动. 底盘控制芯片为STM32F103ZET6,通过RS-485接口与电机驱动器进行通信.
-
图 3展示了果园机器人的整体工作流程. 通过IMU感知自身姿态变换,利用激光雷达获取周围环境点云信息,对点云执行预处理操作:坐标系变换、降采样、去除离群点、滤除地面点云. 利用误差状态卡尔曼滤波器(Error State Kalman Filter,ESKF)融合激光雷达和IMU的数据优化机器人姿态. 获取柑橘果园全局点云地图后进行欧式聚类处理,得到柑橘果树和障碍物的聚类边界,则边界框之外的区域为机器人的安全通行区域,从而可以规划机器人行驶至目标点的最优路线.
规划路线后以ROS系统为导航基础框架,通过NDT-ICP点云匹配获取机器人当前位姿,并输出行驶方向的指令,通过串口发送至STM32单片机,然后STM32单片机通过RS-485接口和底盘电机驱动器通信,应用自校正增量PID控制策略实现机器人的精确控制. 利用上述数据采集和路径规划算法,结合机器人的实时坐标和姿态,成功地实现柑橘园机器人的自主导航功能.
1.1. 丘陵柑橘果园环境分析
1.2. 作业硬件平台
1.3. 工作原理
-
地图构建过程中,机器人坐标系采用三维笛卡尔右手坐标系,其中x方向表示机器人横向,y方向表示机器人航向,z方向表示垂直地面方向,以机器人起始点为世界坐标系原点. 激光雷达坐标系和机器人坐标系重合,IMU的坐标系与机器人坐标系方向一致,仅存在平移转换关系.
激光雷达扫描的原始点云数据经过IMU里程计校正后,可以消除机器人运动时所引发的点云畸变,从而获得周围环境的点云信息[10]. 对原始点云进行地面点的滤除,然后从中提取特征点,用于后续的运动估计和地图构建. 使用最近5帧的数据构建局部地图,将当前帧特征点与局部地图进行匹配,估计机器人的位姿变换. 为提高位姿估计的精度,利用ESKF耦合IMU和激光雷达数据. 将当前帧的点云数据融入到全局地图中,即可获得柑橘果园的全局三维点云地图[11].
-
在丘陵山地,柑橘果园主要分布在具有一定坡度的山丘上. 与平原地区的果园相比,这些果园的地形变化更加显著,地势高低起伏较大. 机器人在这样的地形中运行时,经常面临着频繁的俯仰角、翻滚角及高度方向坐标的变化,导致系统对机器人自身姿态的准确估计变得更加困难,其精度也会受到影响. 地面的不平整性以及高低起伏的变化使得机器人需要适应频繁的姿态调整. 地图构建是机器人自主作业系统运行的基础和前提,地图的精度直接取决于机器人对当前时刻自身姿态的准确感知. 只有基于可靠的自身姿态估计,机器人才能更好地理解和适应地形的高低变化,确保地图构建的准确性和一致性.
因此,解决丘陵山地柑橘果园的机器人运行问题需要综合考虑感知系统的稳定性、对复杂地形的适应能力以及对地图构建的高精度要求. 通过优化姿态感知算法并结合多传感器融合技术,可以提高机器人在这种复杂环境中的自主运行能力,确保果园作业系统的高效运行. 在单独使用激光雷达构建地图时,由于地形起伏,高度方向的误差较大,导致地图精度较低,因此本研究采用ESKF耦合激光雷达对机器人的估计位姿和IMU对机器人的感知位姿[12],以实现对机器人位姿准确且稳定的估计. 相比于传统扩展卡尔曼滤波,ESKF在旋转变换时,状态变量可采用最小化参数表达,用三维变量表达旋转增量,从而减少计算量并提高滤波器效率. 同时它对初始状态的选取和初始协方差矩阵的设置要求较低,能够更好地适应不同的初始条件. 通过使用状态更新公式的雅可比矩阵改善滤波器对非线性系统的收敛性,同时引入扩展状态来描述系统的非线性特征,可降低对线性化假设的依赖性,减小状态估计误差[13].
在ESKF中,状态变量分为真值状态变量、名义状态变量和误差状态变量. 在激光雷达和IMU数据耦合过程中,将激光雷达的初始扫描结果设定为机器人的初始位置和方向. 设ESKF的真值状态变量xt为:
名义状态变量x为:
误差状态变量δx为:
其中:p为当前位置;v为速度;R为机器人姿态;ba为加速度计偏置;bω为陀螺仪偏置;g为重力加速度.
3种状态变量之间的关系为:
在连续时间模型中,误差变量的运动学方程如下:
式中:θ为三轴旋转角度;
$\tilde{a}$ 为直线加速度;$\tilde{w}$ 为角速度;ηa,ηω为IMU测量噪声;ηbω,ηba为IMU偏置模型的高斯噪声.在离散时间模型中,误差变量的运动学方程如下:
在离散时间模型中,误差状态变量δx的运动方程为:
式中:ω为过程高斯噪声;Q为该噪声的协方差矩阵:
式中:ηv为速度计算模型的高斯噪声;ηθ为旋转角度计算模型的高斯噪声.
运动方程的线性化形式为:
式中:F为线性化后的雅可比矩阵.
ESKF运行过程如下:
1) 预测过程:预测名义状态以及误差状态:
2) 更新过程:通过激光雷达观测误差变量,k时刻的观测方程为:
式中:zk为观测数据;vk为观测过程高斯噪声;V为该噪声的协方差矩阵.
误差状态的雅可比矩阵Hk为:
卡尔曼增益Kk为:
k时刻误差状态δxk和协方差矩阵Pk的最优估计为:
3) 将误差状态归入名义状态,作为k+1时刻名义状态:
-
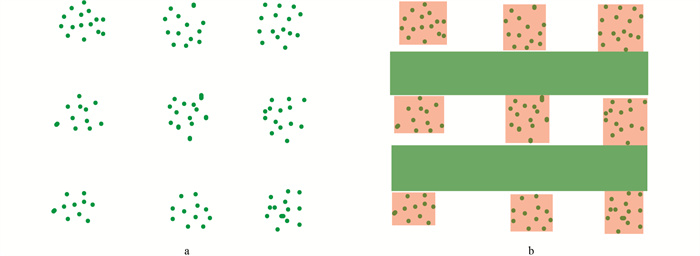
由于果园整体点云数据量较大,在获得三维点云地图后,需要对点云进行体素滤波下采样,即在不损失点云重要信息特征的情况下对点云进行减量,从而加快后续处理计算过程[14]. 对点云数据进行统计滤波处理,以消除噪声点和去除离群点[15]. 经过欧式聚类,成功分离出树冠部分,并对每个独立的聚类计算其矩形边界框,边界框的外部区域即为机器人通行的安全区域[16]. 为提高机器人行驶的安全性,选取树行中最大的边界框,将其设定为当前树行的代表性边界. 图 4为点云处理流程的结果,橙色部分为果树聚类后的边界框,绿色矩形部分为机器人行驶的安全区域.
-
机器人导航系统以周围环境地图、机器人当前位置信息,以及起点和终点坐标为输入,并利用路径规划算法规划出可安全行驶的最优路径. 本研究采用基于多约束条件的路径规划策略. 首先根据全局地图利用A*算法[17]进行全局路径搜索并提取特征点;根据特征点曲率筛选出分段特征点与转弯特征点,并进行特征点优化;以转弯处首末端点约束、底盘转弯半径约束与转向机构延迟约束构建约束条件,以转弯半径曲率均值最小为目标建立B样条曲线并进行参数求解;最后采用三次非均匀B样条曲线表示全局路径[18].
图 5为果园场景的仿真验证结果,黑色矩形为树行膨胀后的障碍物信息. 相较于A*和特征点优化路径,多约束条件路径可以实现在树行中间行驶,并且在换行处曲线行驶,更加符合农业机械作业要求. 实际机械化果园中,同一树行的果树存在间距,但是一般作业机器不会从中穿过,所以将树行整体视为一个障碍物. 同时,为保证作业机械以“U”形运动轨迹遍历果园,分别将障碍物延伸至果园边界形成“U”形长廊式结构.
-
在果园环境中树木密集,三维点云地图数据量较大,所以在定位时加载全局地图的时间代价较大,会导致果园机器人作业效率下降. 在实际定位中,点云配准时并不需要将激光雷达采集到的当前帧点云数据与完整的点云地图进行配准,只需要与当前位置附近的局部点云地图配准即可,所以采用分块存储策略. 将全局点云地图按区域进行划分存储,在机器人初始定位时输入区域标号,将实时点云数据与分块局部地图做匹配,以减少内存消耗,提高定位效率[19].
为确定机器人在果园环境中的具体位置,需要将当前时刻激光雷达扫描得到的点云和先验点云地图进行配准,点云配准的输出是点云之间的变换矩阵. 传统的点云配准方法为迭代最近点法(Iterative Closest Point,ICP)[20],通过最小化2个点云中最近点对的误差之和来确定最优变换矩阵. 目标函数可以表示为:
式中:N表示扫描的点数;R和T分别表示旋转矩阵和平移矩阵;目标函数
$C(\hat{\boldsymbol{R}}, \hat{\boldsymbol{T}})$ 表示变换误差;pi为当前激光雷达扫描点云中点的坐标;qi为先验点云地图中点的坐标.ICP点云配准在周围环境基本不变的情况下表现良好,但是实际生产中基本不变的环境很少,在允许周围环境小部分差异的情况下,可应用正态分布变换(Normal Distribution Transform,NDT)进行处理. NDT是一种基于高斯分布对点进行建模的方法[21],将参考点云(即先验地图)划分为多个单元,每个单元都连续地按高斯分布建模,将点云数据用多维变量的分布形式来表示,此时2个点云之间的配准问题就转换成了求解某个变换参数使得参与变换的点云在参考点云中概率密度之和最大的问题,采用优化的方法求出这个变换参数,即可得到2幅激光点云数据的最优匹配.
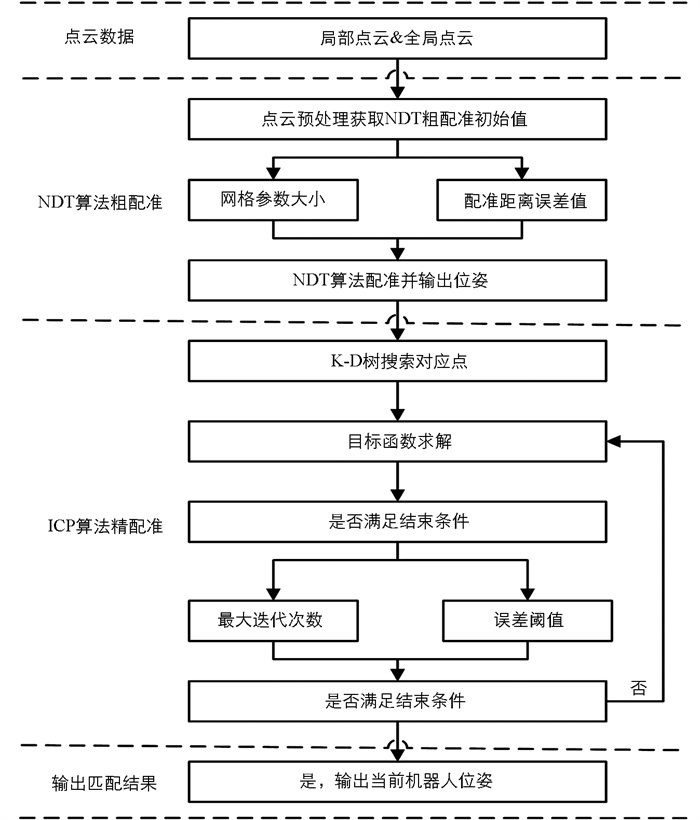
局部点云—全局点云匹配确定机器人在先验全局点云地图中的位姿时,初始值的选取对ICP算法结果的影响较大,当初始值与真实值误差较小时,算法收敛较好. 相反,NDT算法受初始误差的影响较ICP算法略低,因此本文结合ICP和NDT算法进行点云配准定位,点云匹配流程如图 6所示.
2.1. 全局点云地图构建
2.2. ESKF优化位姿
2.3. 点云处理
2.4. 果园路径规划算法
2.5. 基于先验地图的重定位
-
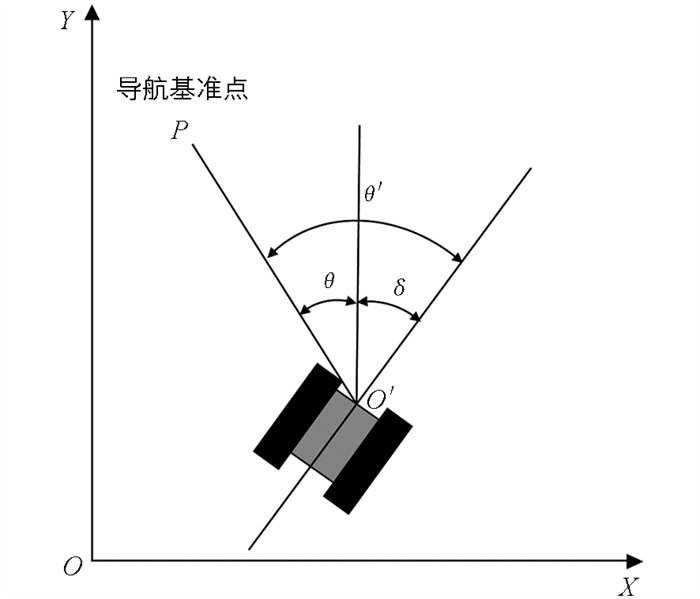
在履带式果园机器人的路径跟踪控制过程中,定义二维全局地图坐标系XOY,其中履带式车辆的前进方向与Y轴之间的角度为航向角[22],如图 7所示. 将整段导航路线分为多段,选取阶段性导航目标点. 履带车在导航目标点处的航向角θ为:
式中:XP和YP为目标导航点的坐标;X0和YO为机器人当前位置坐标.
机器人当前位置航向角与导航目标点处航向角之差θ′为:
式中:θ为机器人在导航目标点处的航向角;δ为机器人当前位置航向角.
-
在现代机电系统中,位置和转角的精确控制是至关重要的,这不仅关乎系统的稳定性,还直接影响其实际应用效果和安全性. 传统的位置PID控制可能会在某些情况下遇到以下问题:系统受到干扰时,控制器可能会过度反应. 为了解决这个问题,引入增量PID控制[23]. 这种方法不是简单地考虑当前误差,而是考虑误差的增量,所以能更好地平衡系统的响应速度和稳定性,使得系统在受到扰动或参数变化时更具鲁棒性.
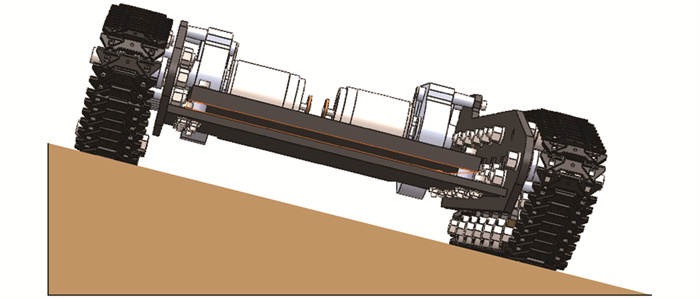
如图 8所示,在丘陵山地果园中,地面不平整会导致机器人在运动过程中经常出现倾斜[24]. 这种倾斜状态会导致两侧履带受力不同,机器人会面临摆动、方向偏移和不均匀负载的情况,从而使得传统的PID控制器在维持稳定性和高控制精度方面面临挑战. 为了应对这些变化,并保持系统的稳定性和最优控制性能,采用递归最小二乘法(Recursive Least Squares,RLS),实时估计系统参数,再利用Ziegler-Nichols整定方法计算PID参数值[25].
在丘陵山地果园中,机器人行进过程中往往伴随着俯仰角度和翻滚角度的变换,并且左右履带的高低不同,会导致电机发生转向和打滑,仅依靠电机编码器数据的反馈会造成较大的误差. 利用卡尔曼滤波器融合电机编码器数据和SLAM系统输出的位姿变换信息,可以提高自校正PID控制器的精度,降低因为履带打滑所造成的误差.
自校正调节(Self-Tuning Regutator,STR)的设计思想,是把未知被控对象参数的估计和控制器的设计分开进行. 自校正增量PID调节器由3部分构成:最小二乘递推参数估计,控制器的参数设计和增量PID调节器,其控制系统结构如图 9所示[26].
-
在离散时间下,对于直线位移的增量式PID控制的公式可以表示为以下形式:
式中:uk为当前时刻的控制量;Kep,TeI,TeD,TeS分别为比例常数、积分时间常数、微分常数和采样周期;ek为k时刻误差,rk为k时刻实际值,yk为k时刻预设值,ek=rk-yk.
在离散时间下,对于差速转角的增量式PID控制的公式可以表示为如下形式:
式中:uθk为当前时刻控制量;Kθp,TθI,TθD,TθS分别为比例常数、积分时间常数、微分常数和采样周期.
-
系统实时参数估计过程中会出现数据饱和问题,即当数据累积到一定数量时,参数估计的准确度反而下降. 所以采用遗忘因子递推最小二乘法,可以对历史数据进行加权,动态地调整历史数据对系统的影响[27].
设系统模型方程为:
式中:y(t)为系统模型输出;φT(t)为系统采样得到的数据信息向量;e(t)为系统噪声;θ为参数向量.
递推最小二乘法是利用系统的输入输出数据{u(t),y(t)},使准则函数J(θ)极小,从而得到参数θ的估计:
为避免对采样值的微小波动过于灵敏而造成控制器参数的不断变化,引入开关变量σ,递推最小二乘法公式如下:
式中:
$\hat{\boldsymbol{\theta}}$ 为参数最优估计向量;K为卡尔曼增益;P为估计误差协方差矩阵;λ为遗忘因子. λ越小,算法的跟踪能力越强,但参数的波动越大,遗忘因子一般选择为0.95<λ<1.
3.1. 航向角控制
3.2. 自校正增量PID控制
3.2.1. 增量式PID控制器
3.2.2. 实时参数估计算法
-
果园机器人的可靠性取决于机器人导航系统的精度,高精度的导航系统是果园机器人能否可靠稳定地完成各类作业的前提. 果园机器人导航性能试验地点位于四川省广安市武胜县扶手村,试验区纵向尺寸为115.3 m,横向尺寸为15.4 m,以试验区地图坐标系的原点为机器人的起点. 机器人在实际柑橘果园中进行试验的场景如图 10所示.
果园机器人性能的评价指标包括建图准确度和导航精度. 建图准确度的衡量标准为所建三维地图与实际环境之间的纵向与横向几何偏差,以及在建图过程中机器人位姿与预定位姿的位置和航向角偏差;导航精度的衡量标准为测量机器人预规划导航路径与机器人实际运动路径的偏差,研究该导航系统精度是否能满足机器人日常巡检作业的需求[28].
-
试验中使用的果园履带机器人如图 11所示,试验过程中设置激光雷达与地面的距离为1 000 mm,惯性传感器与激光雷达布置在同一平面,二者之间的转换只存在平移转换,平移向量为T=[0,0.15,0]. 试验使用RViz软件实现环境信息可视化,验证改进算法的可行性.
-
为了验证ESKF是否能够提高位姿估计的准确性和鲁棒性,设定机器人起点为试验区地图坐标系的原点,控制机器人在初始位置偏差和航向角偏差为零的情况下,以0.8 m/s的速度进行算法优化试验.
试验步骤如下:
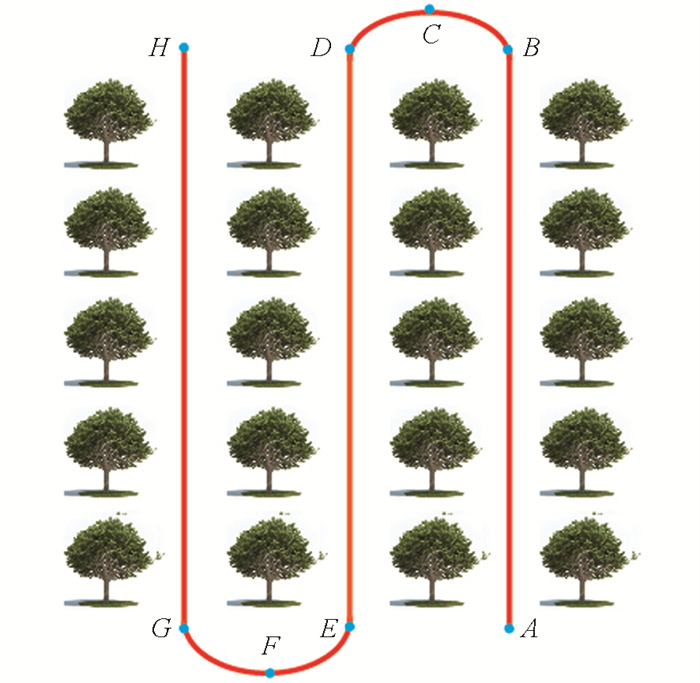
1) 如图 12所示,在果园环境中选择8个检测点A~H,所有检测处均有位移输入和转向输入.
2) 沿着关键点A~H进行地图的构建,在关键点设定预定位姿,并记录关键点的位置和机器人姿态.
3) 在地图构建过程中,为保证尽可能小的测量误差,同时开启2个算法框架(使用ESKF和不使用ESKF)进行地图构建.
4) 重复进行多次试验,并将试验数据进行滑动均值滤波,消除异常点的干扰,分析ESKF优化特性.
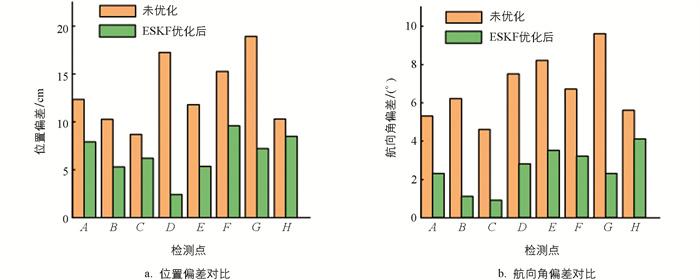
地图尺寸信息试验结果如表 1所示,未进行优化的地图系统测量累积误差为6.61 m,经过ESKF优化后的地图测量累积误差为1.96 m. 在建图过程中,图 13展示了系统感知的机器人位姿与机器人实际位姿的偏差,未优化时机器人在关键点的平均位置偏差为13.57 cm,平均航向角偏差为6.43°. 而优化后的平均位置偏差为6.54 cm,平均航向角偏差为2.53°. 通过对比可以明显观察到,ESKF优化使得系统对机器人位姿的感知更为准确,地图精度显著提高,可以为后续导航环节提供有力的支持.
-
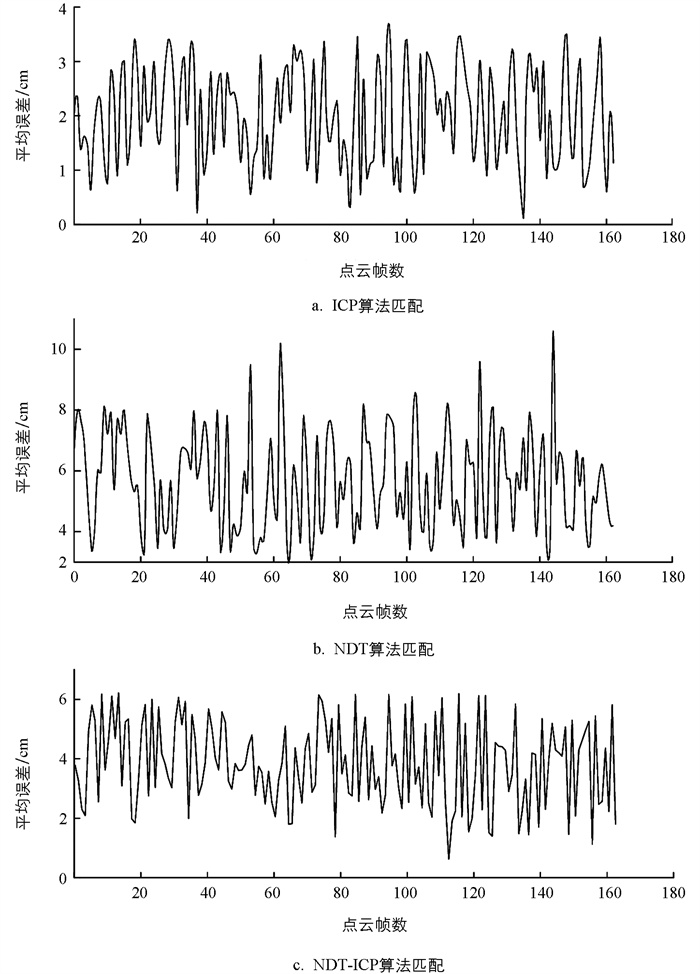
为验证NDT-ICP算法在果园环境下进行点云配准定位的可靠性,以试验区地图坐标系的原点为机器人出发的起点进行试验分析. 分别利用NDT、ICP和NDT-ICP对相同的163帧点云数据和全局点云进行配准,多次循环,并记录点云配准的效率和误差. 点云匹配效率试验时,设定点云配准的误差阈值为2 cm,记录配准每帧点云的消耗时间. 点云精度试验时,设定点云配准的最大循环次数为1 000次,点云配准的误差阈值为0.01 cm,记录配准每帧点云的误差.
由表 2对3种算法点云配准定位效率的对比分析可知,NDT-ICP算法的配准效率介于NDT和ICP算法的配准效率之间,平均每帧耗时为0.53 s.
由图 14对点云配准误差对比分析可知,NDT-ICP算法的误差也介于ICP算法和NDT算法的配准误差之间,平均配准误差为4.72 cm. 由以上分析可知,NDT-ICP点云配准算法兼具高效率和高准确性,可以满足柑橘果园机器人的定位需求.
-
为了验证航向角的控制策略及RLS自适应参数PID转向角增量控制的有效性,机器人以试验区地图坐标系的原点为起点,获取预定的规划路径和阶段性导航目标点. 随后机器人以0.5 m/s,0.8 m/s,1.2 m/s的行驶速度分别进行5次试验,分别测量转弯目标点与直线目标点处的轨迹偏差,以此对导航系统的性能进行系统性的评估和验证. 试验结果如表 3所示,随着速度的增大,目标点平均位置偏差和航向角偏差均增大. 行驶速度为1.2 m/s时,直线行驶平均位置偏差为0.18 m,最大位置偏差为0.23 m,平均航向角偏差为4.2°,曲线转弯处平均位置偏差为0.38 m,最大位置偏差为0.57 m,平均航向角偏差为16.7°,果园平均行间距约为4 m,所以在1.2 m/s的速度下仍能满足自主导航作业要求.
4.1. 试验平台
4.2. 试验设计与结果分析
4.2.1. 算法优化试验
4.2.2. 点云匹配定位试验
4.2.3. 路径跟踪试验
-
1) 利用激光雷达和IMU传感器实现了果园自主导航系统的构建,并采用了ESKF来进一步优化建图过程中机器人的位姿. 对点云进行处理,利用NDT-ICP算法实现了机器人基于先验全局点云地图的定位. 试验结果表明,通过该优化策略,机器人对自身姿态感知的平均位置和角度偏差分别为6.43 cm和2.53°,说明该优化算法可以提供较为精准的自身位姿信息和周围环境地图,为后续导航提供支持.
2) 在地图构建与自身定位算法的基础上,设计了基于预瞄点的航向角控制系统,为了应对果园地形的变化,采用了实时调整增量式PID参数的路径跟踪控制策略. 为了验证其效果,在履带式底盘上进行了不同速度下的控制试验. 在速度最高时控制系统的平均位置偏差和角度偏差均可满足要求,说明该控制策略在3种不同的行驶速度下均能实现对预定路径的跟踪,满足果园机械自主导航作业需求.
丘陵山地柑橘果园机器人导航控制系统实现了果园环境地图构建、全局路径规划和路径跟踪,为柑橘果园作业机械的自主导航提供了技术支持. 下一步将开展自主作业过程中面对不同障碍物的实时避障与绕行问题研究,从而进一步拓宽果园机器人的使用场景.




 下载:
下载: