-
高光谱图像(Hyperspectral Image,HSI)是由描述地物空间关系的二维空间数据和确定地物性质的一维光谱数据组成的三维数据[1],具有图谱合一和光谱分辨率高的特点,能够从大范围的电磁光谱中收集和处理数据[2]. HSI最显著的特征是光谱分辨率能力大幅提高,精细的光谱分辨率可以反映地物光谱的细微特征,被广泛应用于地球遥测、太赫兹成像和医学成像等多个领域中[3-4].高光谱图像的噪声对数据分析带来的不利影响严重制约了高光遥感技术的发展[5],因此研究高光谱图像去噪成为图像处理方法的热点之一.
HSI去噪是提高后续高光谱数据分析和应用性能的关键预处理过程,其要求在恢复光谱分辨强度(幅度)信息的同时,恢复光谱分辨率的相位信息[6-7].目前HSI去噪的方法主要分为光谱域去噪、空间域去噪和空间谱间联合去噪[8].光谱域最常用的去噪技术是最小噪声分离、Savitzky-Golay滤波及小波方法,可以消除噪声对光谱分析的影响[9]. HSI在空间域是一幅二维图像,各个波段的图像可以使用经典的图像去噪方法[10].由于高光谱数据的三维性,只采用空间域或光谱域的HSI去噪只能滤除噪声图像中的大部分噪声[11],不能很好地处理低信噪比的高光谱数据,因此,研究者更倾向于光谱域和空间域相结合的高光谱数据去噪.
文献[12]提出了一种基于低秩和稀疏表示的高光谱图像快速去噪方法,该方法利用高光谱图像子空间的低维性和其表示系数的自相关性,基于非局部块匹配的方法对图像进行去噪.此方法具有速度快和鲁棒性高等特点,可以有效去除高斯和泊松噪声.文献[13]提出了一种基于空间谱深度残差卷积神经网络的高光谱图像去噪方法,该方法使用深度卷积神经网络学习噪声和高光谱图像之间的非线性端到端映射,然后分别采用多尺度特征提取和多级特征表示,来捕获多尺度空间光谱特征和融合不同的特征表示以进行最终恢复.文献[14]提出了一种基于非局部相似度的非负Tucker分解的高光谱图像去噪方法,对空域的非局部相似性和光谱域的全局相似性进行建模.它利用高光谱图像在合适窗口大小中的非局部相似性,将高光谱图像中提取的三维全波段图像块分组以形成三阶张量,最后基于分层最小二乘的非负Tucker分解进行求解,从而达到较好的去噪效果.
在研究了现有HSI去噪的基础上,为了进一步提高噪声鲁棒性和去噪效果,本文提出了一种基于复值特征子空间的高光谱图像去噪方法.该方法首先对复值信号和噪声相关矩阵进行初步估计,然后利用高光谱数据的奇异值分解定义了一个最优的低维特征子空间,最后利用复域块匹配3D滤波器(Complex-Domain Block-Matching 3D,CDBM3D)对最优特征子空间的图像进行滤波,滤波后的特征图像用于重建高光谱数据.由于高光谱图像块的相似性,特征空间的维数远小于高光谱数据立方体的长度,从而简化了高光谱数据的处理过程并提高了算法的速度.实验结果表明,提出的方法可以稳定有效地对干涉相位和包裹相位的高光谱数据进行去噪,能够恢复整个高光谱立方体丢失的数据,具有较强的鲁棒性.
全文HTML
-
设
$ U(x, y, \lambda) \subset C^{N\times M}$ 是(x,y)上提供固定波长λ的大小为N×M的复值高光谱图像立方体的切片,${{Q}_{\mathit{\Lambda} }}(x, y)=\{U(x, y, \lambda ), \lambda \subset \mathit{\Lambda} \}, {{Q}_{A}}\subset {{C}^{N\times M\times {{L}_{\mathit{\Lambda} }}}} $ 是由一组波长Λ与单个波长的个数LΛ组成的整体立方体.因此,立方体的总大小是N×M×LΛ像素.QΛ(x,y)是包含与具有坐标(x,y)的场景相对应的LΛ光谱观测值.将在加性噪声假设下的高光谱去噪问题的观测值定义如下:
其中,ZΛ为记录的有噪高光谱数据,QΛ为无噪HS数据,
$ {{\varepsilon }_{\mathit{\Lambda} }}\subset {{C}^{N\times M\times {{L}_{\mathit{\Lambda} }}}}$ 为加性噪声.空间坐标(x,y)是分别属于范围[1,N]和[1,M]的整数.根据无噪图像的表示法,噪声立方体可以用切片Z(x,y,λ)表示为${{Z}_{\mathit{\Lambda} }}(x, y)=\left\{ {{Z}_{\mathit{\Lambda} }}(x, y, \lambda ), \lambda \in \mathit{\Lambda} \right\}, {{Z}_{A}}\subset {{C}^{N\times M\times {{L}_{\mathit{\Lambda} }}}} $ .将去噪问题表示为根据给定的ZΛ(x,y)重建未知的QΛ(x,y).无噪高光谱的QΛ(x,y)和噪声εΛ(x,y)的属性对算法开发至关重要.
以下3个假设是本文的基本假设:
高光谱切片U(x,y,λ)对附近波长λ的相似性源于U(x,y,λ)是λ的缓慢函数; 高光谱图像U(x,y,λ)作为(x,y)的函数的稀疏性意味着存在这样的基,使得U(x,y,λ)可以用这些基的少量元素来表示; 噪声εΛ(x,y)是具有对角相关矩阵LΛ×LΛ的零均值循环对称复高斯,干净的图像子空间识别是本文算法至关重要的第一步.
-
复域块匹配3D(Complex-Domain Block-Matching 3D,CDBM3D)滤波器能够分别对每个波段的高光谱立方体的图像进行滤波,其结果可以表示为
其中,
$ \hat{U}(x, y, \lambda)$ 是干净未知波阵面U(x,y,λ)的估计,f表示CDBM3D滤波器.本文将CDBM3D作为MATLAB工具箱复域BM3D算法的通用名称,这些算法是实值块匹配3D滤波器复域的推广. CDBM3D算法由阈值滤波和维纳滤波2个连续的阶段组成,每个阶段包括:分组、3D/4D高阶奇异值分解(HOSVD)分析、硬阈值滤波、HOSVD逆变换和聚合.在维纳滤波阶段,用维纳滤波代替阈值选取.具体流程图见图 1.
第一阶段,阈值滤波得到基本估计:
1) 基于块匹配的图像分组:将在固定λ下拍摄的噪声图像
$ Z(x, y, \lambda) \subset C^{N \times M}$ 分割为重叠的矩形小块,大小为N1×M1.对于每个块,本文基于块匹配在Z(x,y,λ)中搜索参考块的相似块,识别它们并将它们堆叠在3D组(数组,张量)中,形成一个四维矩阵.2) 硬阈值滤波:对形成的四维矩阵进行高阶奇异值分解(HOSVD),实现核心张量的阈值化(硬阈值归0),通过硬阈值滤波的方法减弱噪声,最后使用阈值核心张量的逆向HOSVD得到四维组中所有图像块的基本估计.
3) 图像块重组:将所有重叠块估计值进行聚合以获得经过加权的逐组估计值,从而得到改进图像的基本估计值.
第二阶段,维纳滤波得到最终估计:阈值滤波后的图像是维纳滤波的输入信号,可以提高分组精度,再基于维纳滤波器对图像进行去噪.
1) 图像块分组:基于块匹配在第一阶段寻找到当前参考块的相似块位置,基于这些相似块的位置获得一个来自图像噪声的四维矩阵和一个来自第一阶段的四维矩阵.
2) 维纳滤波:对这2个四维矩阵分别应用HOSVD变换,对四维矩阵进行维纳滤波处理,并将滤波后的数据进行HOSVD逆变换,得到所有图像块的估计值.
3) 图像块重组:将所有重叠块估计值进行聚合以获得经过加权的逐组估计值,从而得到改进图像的基本估计值.
CDBM3D同时处理相位和幅度时考虑高光谱数据常见的相关性,在幅度和相位的分段滤波中忽视其相关性,并且其基函数是自适应变化的,从而提高了估计的精度. CDBM3D算法是在波段Z(x,y,λ)中寻找相似块,识别它们并一起处理.这种相似性概念允许基于功能强大的现代稀疏逼近工具来设计有效的去噪方法.
-
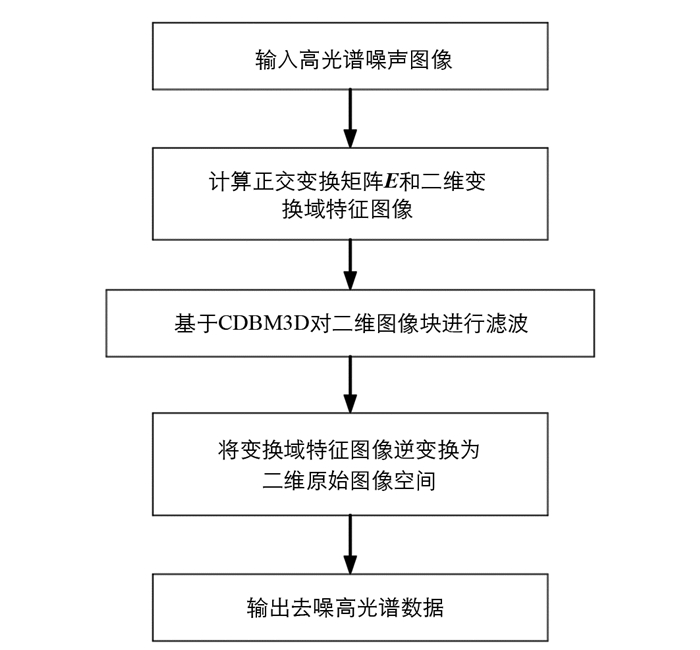
本文提出了一种用于高光谱图像去噪的复域立方体滤波(Complex Cube Filter,CCF)算法,来联合处理高光谱立方体的所有波段图像.该算法首先初步估算复域信号和噪声的正交变换矩阵,然后在最小二乘误差意义下选择最能代表信号子空间的奇异值分解(SVD)特征向量的特征子集,最后基于CDBM3D滤波对特征图像进行滤波.本文算法的具体流程见图 2.
本文CCF算法与以下表示一起使用:
其中,
$ {\bar{\mathit{\Lambda} }}$ 是一组要去噪的图像块.对于滑动滤波,$ {\bar{\mathit{\Lambda} }}$ 定义为以宽度δλ0,λ0为中心的对称波长间隔λ.复域立方体滤波CCF联合处理立方体
${{Z}_{{\bar{\mathit{\Lambda} }}}}(x, y) $ 的数据,并提供所有$ \lambda \in \bar{\mathit{\Lambda} }$ 的估计${{\overset\frown{U}}_{{\bar{\mathit{\Lambda} }}}}(x, y) $ . -
输入3D数据立方体
$\left\{ {{Z}_{{\bar{\mathit{\Lambda} }}}}(x, y) \right\}:N\times M\times {{L}_{{\bar{\mathit{\Lambda} }}}} $ ,并初步将其重塑为大小为$ L_{\bar{\mathit{\Lambda}}} \times N M: N \times M \times L_{\bar{\mathit{\Lambda}}} \rightarrow L_{\bar{\mathit{\Lambda}}} \times NM$ 的2D矩阵Z.式(5)是对正交变换矩阵$\boldsymbol{E} \subset C^{L_{\bar{\mathit{\Lambda}}} \times p} $ 和2D变换域特征图像Z2,eigen的求解方式.式中,HySime[12]适用于基于奇异值分解(SVD)的最小误差高光谱信号子空间识别,p为特征空间的长度,HySime根据最小二乘法原理,最小化图像数据与噪声数据的投影误差之和. HySime识别用于高光谱图像表示的最佳子空间,包括特征空间p的维数和E的列.给定E时,特征图像计算可表示为
将大小为p×MN的2D变换域Z2,eigen重塑为大小为
$N \times M \times p: p \times N M \rightarrow N \times M \times p $ 的3D图像域阵列Z3,eigen. -
使用复域块匹配3D(Complex-Domain Block-Matching 3D,CDBM3D)滤波器分别对每个波段的高光谱立方体的图像进行滤波.用CDBM3D算法对Z3,eigen的N×M个2D图像(切片)进行滤波,其结果可以表示为
其中,
${{\overset{\wedge }{\mathop{Z}}\, }_{3, { eigen }}}\left( x, y, {{\lambda }_{s}} \right) $ 是干净未知波阵面Z3,eigen(x,y,λs)的估计,p个特征值λs属于特征空间Λ,f表示CDBM3D滤波器.随后将3D数组
${{\overset{\wedge }{\mathop{Z}}\, }_{3, { eigen }}}\left( x, y, {{\lambda }_{s}} \right) $ 重塑为大小为p×MN的2D变换域Z2,eigen. -
将变换域的特征图像
${{\overset{\wedge }{\mathop{Z}}\, }_{3, { eigen }}}\left( x, y, {{\lambda }_{s}} \right) $ 逆变换到大小为p×NM的2D原始图像空间,如公式(9)所示,它是公式(6)的逆变换.将2D图像
$ {{\overset{\wedge }{\mathop{Z}}\, }_{2}}$ 重塑为立方体大小N×M×LΛ,它给出了相应的滤波立方体${{\overset{\wedge }{\mathop{U}}\, }_{{\bar{\mathit{\Lambda} }}}}(x, y) $ .这些向前和向后重塑通道
$2 \mathrm{D} € 3 \mathrm{D} $ 允许在2D变换域中对特征空间Z2,eigen进行细化,并在相应的3D域Z3,eigen中逐块产生CDBM3D滤波.基于SVD的HySime解决了噪声协方差矩阵的估计以及信号子空间的优化问题,使干净的高光谱
$ {{U}_{{\bar{\mathit{\Lambda} }}}}(x, y)$ 与其估计值之间的均方误差最小.在本文算法中使用了(x,y)上的平均协方差rλ,λ′(x,y)和高光谱图像的初步估计,子空间的优化可以最大限度地减小子空间的规模,并且通常使得到的子空间维数$p=L_{\bar{\mathit{\Lambda}}} $ 最小化,这简化了高光谱数据的处理过程,并提高了算法的速度.因此,CDBM3D滤波仅对p特征图像进行滤波,但是逆变换公式(9)给出所有$L_{\bar{\mathit{\Lambda}}} $ 光谱图像的估计.本文使用CDBM3D算法对特征图像进行滤波,复值图像的虚部和实部用于3D分组数据的4D HOSVD分析,该算法包括阈值和维纳滤波2个阶段,从而使该算法具有更高的性能.
3.1. 计算变换矩阵和特征图像
3.2. 复域块匹配3D滤波器去噪
3.3. 将变换域图像逆变换到二维空间
-
所有实验在一台配置为Intel Corei5@1.6 GHz和4 GB RAM的Windows 10 Pro的笔记本上进行,并在MATLAB 2014a环境下实现.采用透射式高光谱数字全息术获得实验的高光谱数据,从中截取大小为807×807×226(宽度×高度×波段数)的图像块作为实验数据.研究对象是透明幻灯片,光源是白色LED,LED强度较弱的光谱区域全息图的信噪比较低,LED强度较高的区域信噪比较高.为了验证本文方法的有效性,将本文方法与均值滤波平滑法(AVE)[15]、块匹配3D滤波器(BM3D)[9]、文献[12]、文献[13]进行比对分析.
所有实验主要针对的加性噪声是具有标准差σ的独立同分布的零均值循环对称复高斯.为了选择合适的窗口大小,针对具有双峰相位的对象进行实验,选择高度较小的峰使得相位变化不超出高光谱立方体所有切片的包裹范围.为了评价本文算法的性能,本文计算每个波段去噪后的图像与原图像的相对均方根误差(RRMSE),去噪后的图像与原始图像越相似则RRMSE值越小,RRMSE可表示为
其中,
$ {{\overset{\wedge }{\mathop{\varphi }}\, }_{est\text{ }}}$ 为重构相位,φtrue为无噪相位.PSNR表示滤波图像的最大像素与噪声的比值,定义为
其中,M表示均方误差,fmax和fmin分别表示去噪图像的最大和最小像素. PSNR值越大,说明去噪图像失真越小,图像的去噪效果越好.
基于感知模型的归一化度量SSIM定义为
其中,
$ l(x, y)=\frac{2 u_{x} u_{y}+c_{1}}{u_{x}^{2}+u_{y}^{2}+c_{1}}, c(x, y)=\frac{2 \sigma_{x} \sigma_{y}+c_{2}}{\sigma_{x}^{2}+\sigma_{y}^{2}+c_{2}}, s(x, y)=\frac{\sigma_{x y}+c_{3}}{\sigma_{x} \sigma_{y}+c_{3}}$ 分别表示亮度比较、对比度比较和结构比较,x,y分别为参考图像和待测图像,$u_{x}, u_{y}, \sigma_{x}^{2}, \sigma_{y}^{2}, \sigma_{x y} $ 分别表示图像x,y的均值、方差和协方差,c1,c2,c3为很小的常数.平均峰值信噪比(Mean peak signal-to-noise ratio,MPSNR,定义为PM)和平均结构相似性(Mean Structural SIMilarity,MSSIM,定义为SM)衡量图像的去噪效果,MPSNR值越大,则去噪效果越好; MSSIM值越接近1,去噪效果越好,计算公式如下所示
其中,N表示高光谱图像的波段数.
为了说明滤波的正确性,本文比较了3幅图像:①来自有噪声的未滤波高光谱立方体中波长为446 nm的图像; ②来自高光谱立方体中相同的噪声图像,但使用本文算法进行滤波; ③对于相同的测试对象,在相同的光学装置中获得的未经滤波的波长为446 nm的图像,但在另一个实验中具有更高的信噪比.这种比较对于测试重建图像的正确性和高光谱立方体其他切片中可能出现的伪像是非常重要的.
图 3(a)和图 3(d)为噪声图像,图 3(b)和图 3(e)为使用本文所提方法滤波后的图像,图 3(c)和图 3(f)为高信噪比的噪声图像.可以看出,本文所提方法可以将噪声图像中几乎完全丢失的信息较好地恢复出来,并且滤波后的幅度/相位特征与在较高信噪比切片(图 3(c)和图 3(f))中清晰可见的结构特征一致.这是因为本文方法对所有图像进行联合去噪,恢复了整个高光谱立方体中丢失的数据,包括低信噪比的波段图像.因此,本文方法对噪声数据具有较强的鲁棒性.
图 4和图 5给出了对干涉相位复合图像和包裹相位图像进行滤波时,不同去噪方法的全波段RRMSE值的比较结果.可以看出,本文方法具有最佳性能,尽管在波长间隔不同部分的相位图像之间存在很大差异,本文算法仍可以实现所有波长的高质量去噪.这是因为所提方法利用CDBM3D同时对噪声图像的相位和幅度进行去噪,并且其基函数是自适应变化的,从而提高了估计的精度.
表 1给出了本文算法、BM3D、文献[12]和文献[13]去噪后的平均峰值信噪比(MPSNR)和平均结构相似性(MSSIM).从MPSNR和MSSIM指标可以看出,本文算法去噪后的图像与原图像更加相似,去噪后的图像结构相似度更高.
-
本文提出了一种基于复值特征子空间的高光谱图像去噪方法.该方法首先对复值信号和噪声正交变换矩阵进行初步估计,然后基于观测到的复值数据奇异值分解(SVD)定义了一个最优的低维特征子空间,最后利用复域块匹配3D滤波器和维纳滤波对最优特征子空间的图像进行滤波,滤波后的特征图像用于重建高光谱数据.实验结果表明,所提算法对噪声数据具有很强的鲁棒性,即使在低信噪比的情况下也能有效地恢复高光谱立方体中丢失的信息,并且提供了无需相位包裹的噪声抑制.本文方法假设搜索相似的图像块,然后将其组合在一起进行滤波,这步骤使得本文算法不局限于噪声滤波.未来的工作是将其开发为针对各种干扰进行图像重建的通用工具.




 下载:
下载: