假设总人群的接触网络是一个无标度网络，一个节点表示一个人，网络上的连边表示人与人之间的接触. 我们作如下假设：

1) 整个网络的出生率和自然死亡率分别为A和d，并且出生的个体都为易感染者. 依据文献[14]，添加和删除节点和边在网络中只占很小的比例，对网络结构的改变很小，因此可以假设网络上的总节点数N是不变的，是静态的，也就是A=d.

2) 网络上的人分为4类：易感染者S(Susceptible)、感染者I(Infected)、隔离者Q(Quarantine)、恢复者R(Recovered). 令S_k(t)，I_k(t)，Q_k(t)和R_k(t)分别代表度为k的易感染者、感染者、隔离者和恢复者在t时刻的相对密度. 标准化后，S_k(t)+I_k(t)+Q_k(t)+R_k(t)=1.

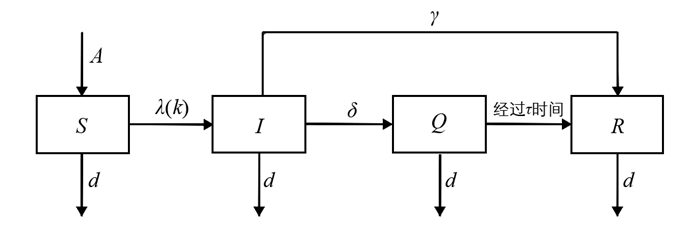
3) 每个易感染者S都有概率λ(k)(与节点的度k有关)被感染者感染，成为感染者I. 感染者I有概率δ被隔离，成为隔离者Q. 感染者I同时有概率γ恢复健康，成为恢复者R. 隔离者Q经过τ时间的隔离治疗后，成为恢复者R.

基于以上假设，可建立SIQR模型的仓室框图(图 1)，对应的微分方程系统如下：

其中λ(k)为感染率，其形式一般有如下两种^[14]：λk，λc(k). Θ(t)代表一个度为k的易感染者每次接触感染者的概率^[14]，其形式如下：

其中p(k)是网络的度分布；$\langle k\rangle=\sum_{k=1}^{n} k p(k)$是网络的平均度；φ(k)=ak^α·(1+bk^α)^-1是度为k的感染者的非线性传染系数，其参数0≤c≤1，a>0，b≥0.

给出系统(1)的初始条件

其中

由泛函微分方程的基本理论^[18]易知在初始条件(3)下，系统(1)存在唯一解，并且当t≥0时，系统(1)存在唯一正解. 同时，不难得出区域Ω是系统(1)的正向不变集，本文将在Ω内讨论系统(1)的性态.

建立模型后，需得出疾病的基本再生数R₀^[18]，即单位病程内一个病人所传染的人数. 当R₀ < 1时，一个病人在单位病程能传染的人数小于1，疾病将自然消失，不会流行；当R₀>1时，一个病人在单位病程能传染的人数大于1，疾病将持久存在，成为流行病.

定理1   令

其中$\langle\lambda(k) \varphi(k)\rangle=\sum_{k=1}^{n} \lambda(k) \varphi(k) p(k)$，则以下结论成立：

1) 系统存在无病平衡点E⁰

其中$S_{k}^{0}=\frac{A}{d}, I_{k}^{0}=0, Q_{k}^{0}=0, R_{k}^{0}=0$，k=1，2，3，…，n.

2) 当R⁰>0时，系统(1)存在地方病平衡点E^*

证   由系统(1)中的方程组，不难得出系统(1)始终存在无病平衡点E⁰

接下来，假设系统存在地方病平衡点E^*，

则E^*满足系统(1)

其中，

解方程组(5)，得到

将I_k^*带入(6)式，得到

显然，Θ^*=0是平凡解. 当Θ^*≠0时对(8)式两边同除以Θ^*，研究函数

注意到$\dot{f}\left({\mathit{\Theta}}^{*}\right)>0$，且$\lim\limits _{\mathit{\Theta} \rightarrow+\infty} f(\mathit{\Theta})=1$. 根据零点定理，如下条件成立时，方程f(Θ)=0存在唯一正解，

因此，我们定义基本再生数R₀如下

综合上述分析，当R₀>1时，系统(1)存在地方病平衡点E^*.

注1  由R₀的表达式得出，R₀与出生率A，感染率λ(k)和非线性传染系数φ(k)正相关，与死亡率d，恢复率γ和隔离率δ负相关.

注2   由(7)中正平衡点的表达式，不难看出τ不影响I_k^*和S_k^*的值，而影响Q_k^*和R_k^*的值. 也就是说，隔离周期的长短影响隔离者和恢复者的最终人数. Q_k^*随着τ的增大而增大，R_k^*随着τ的增大而减小.

定理2   当R₀ < 1时，系统(1)的无病平衡点E⁰全局渐近稳定.

证   由(4)式知，0≤S_k(t)≤ $\frac{A}{d}$，定义Lyapunov函数

计算V(t)沿系统(1)的导数可得

因此，当R₀ < 1时，有$\left.\dot{V}(t)\right|_{(1)} \leqslant 0$. 并且，当且仅当I_k(t)=0时，$\left.\dot{V}(t)\right|_{(1)}=0$，根据(1)式得$\lim\limits _{t \rightarrow+\infty} S_{k}(t)$=1，$\lim\limits _{t \rightarrow+\infty} Q_{k}(t)$=0，$\lim\limits _{t \rightarrow+\infty} R_{k}(t)$=0. 根据LaSalle不变集原理^[20]，系统(1)的无病平衡点E⁰是全局渐近稳定的.

定理3   当R₀>1时，系统(1)的地方病平衡点E^*全局渐近稳定.

证   注意到，系统(1)中的前两个方程不涉及Q(t)和R(t)，由此，只需考虑如下系统：

其中

联合(9)式和(5)式，得到

考虑如下函数

U(t)沿系统(9)求导，得

定义函数

注意到当x>0时，G(x)≥0，当且仅当x=1时，等号成立. 则(11)式可化为

考虑如下两个矩阵

因为矩阵B是一个不可约矩阵，B是B的Laplacian矩阵，根据文献[21]的结论，B也是不可约矩阵. 则线性系统Bv=0，存在正解

其中C_kk是矩阵B的第k个对角线元素，k=1，2，3，…，n. 由此得到

即

现在定义Lyapunov函数

根据(11)，(12)和(13)式，得到$\left.\dot{V}(t)\right|_{(1)} \leqslant 0$. 当且仅当S_k(t)=S_k^*和I_k(t)=I_k^*时，等号成立，同时由(1)式得$\lim\limits _{t \rightarrow+\infty} Q_{k}(t)$=Q_k^*，$\lim\limits _{t \rightarrow+\infty} R_{k}(t)$=R_k^*. 根据LaSalle不变集原理^[20]，系统(1)的地方病平衡点E_k^*是全局渐进稳定的.

注3   当A=0，d=0，λ(k)=λk，φ(k)=k，并取时滞τ=ε^-1，时滞微分系统(1)简化为文献[22]中的常微分系统(1). 此时基本再生数的表达式R₀=λ〈k²〉·[〈k〉(γ+δ)]^-1，结论与文献[22]一致.

为验证结论的正确性，我们对模型(1)进行数值模拟. 取节点最大度值n=200，最小度值m=1，总节点数N=20 000. 网络上的度分布符合幂律分布p(k)=Ck^-γ(2 < γ≤3)，其中γ=2.5，经过计算，节点度为1~200的截断误差为0.04%，在合理范围之内. 取C≈0.745 5以满足$\sum_{k=m}^{n} p(k)$=1. 非线性传染系数φ(k)=ak^α·(1+bk^α)^-1，取a=0.5，α=0.75，b=0.02，感染率λ(k)=λk.

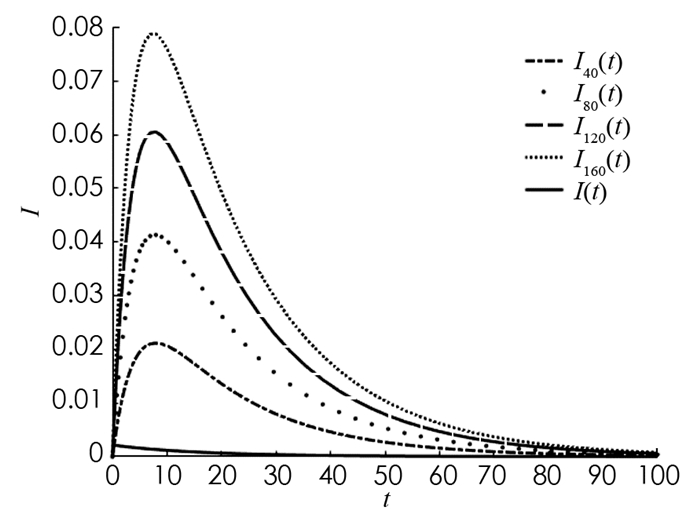
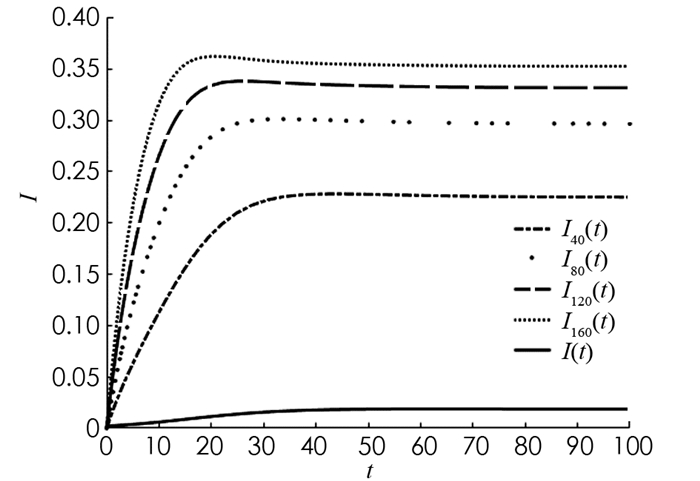
令$I(t)=\sum_{k=m}^{n} p(k) I_{k}(t)$，表示感染者的平均密度，类似地，S(t)，Q(t)，R(t)分别代表易感染者、隔离者、恢复者的平均密度. 取初始值如下：I₅(η)=0.1，I₆(η)=0.1，I_k(η)=0，k≠5，6.

取λ=0.1，A=0.1，d=0.1，τ=3，δ=0.1，γ=0.03，则R₀≈0.774 1 < 1. I₄₀(t)，I₈₀(t)，I₁₂₀(t)，I₁₆₀(t)和I(t)随时间t的变化趋势见图 2，可以看出当R₀ < 1时，疾病逐渐消失. 取λ=0.2，A=0.1，d=0.1，τ=3，δ=0.1，γ=0.03，则R₀≈1.548 2>1. I₄₀(t)，I₈₀(t)，I₁₂₀(t)，I₁₆₀(t)和I(t)随时间t的变化趋势见图 3，可以看出当R₀>1时，疾病持续存在，并且逐渐趋向到一个稳定值. 图 2和图 3分别验证了定理2和定理3.

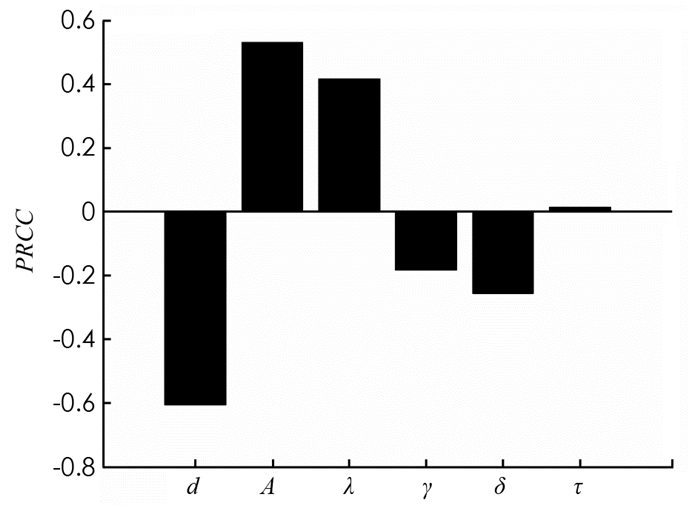
最后，我们进行参数敏感性分析，用PRCC(偏秩相关系数)检测基本再生数R₀对于参数的依赖性. 取样本空间n=1 200，计算6个影响R₀参数的PRCC值. 如图 4所示，λ和A对R₀有正影响，d，γ，δ对R₀负影响，而R₀对τ不敏感. 图 4验证了注1中对R₀表达式的说明. 因此，增大隔离率δ，提高恢复率γ，降低感染率λ可以控制疾病传播.

为了研究隔离周期对传染病的影响，本文基于无标度网络建立了具有时滞的SIQR传染病模型，其中时滞代表平均隔离周期. 通过微分方程定性与稳定性理论，得到了疾病传播的基本再生数. 通过构造Lyapunov函数，证明了当R₀ < 1时，无病平衡点是全局渐近稳定的；当R₀>1时，地方病平衡点是全局渐近稳定的. 最后，对模型进行数值模拟，验证了结论的正确性，并对不同参数进行了敏感性分析. 研究结果表明隔离周期的长短不影响易感染者和感染者的最终人数，但是影响隔离者和恢复者的最终人数. 基于R₀的表达式以及不同参数的PRCC值，得出控制疾病传播的有效方法为增大隔离率，提高恢复率和降低感染率.